

 次: 合同方程式の解法
上: 合同式
前: 合同式
次: 合同方程式の解法
上: 合同式
前: 合同式
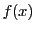 が整数係数の整式であるとき,
が整数係数の整式であるとき,
を合同方程式と呼ぶ.
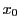 をこの合同式を満たす一つの整数とし,
をこの合同式を満たす一つの整数とし, 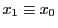 とすれば,定理10より
とすれば,定理10より
である.すなわち を法として
を法として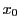 と合同な数はすべてこの合同方程式の解である.
と合同な数はすべてこの合同方程式の解である.
以下,合同方程式の解とはその合同方程式を満たす を法とする剰余類のこととする.
合同方程式を解くとは,それを満たす剰余類を求めることとする.
簡単に「合同式を解く」ともいう.
を法とする剰余類のこととする.
合同方程式を解くとは,それを満たす剰余類を求めることとする.
簡単に「合同式を解く」ともいう.
合同方程式のすべての解を求めようとすれば,
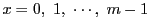 の
の 個の値を代入してみればよい.つまりどんな合同方程式の解も,有限回の計算で求めることが出来る.
その意味で解を有理整数にかぎるなら,必ず解ける.
そのうえで,解の存在とより少ない手順で解を構成する方法を調べよう.
個の値を代入してみればよい.つまりどんな合同方程式の解も,有限回の計算で求めることが出来る.
その意味で解を有理整数にかぎるなら,必ず解ける.
そのうえで,解の存在とより少ない手順で解を構成する方法を調べよう.
まず一次合同方程式について考える.
定理 12
一次合同方程式
は
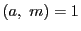
のときただ一つの解がある.
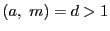
のときは,

が

で割り切れるときにかぎって解がある.
その解の個数は

である.■
証明
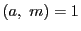 のとき.
のとき.
を を法とする剰余系とする.このとき
を法とする剰余系とする.このとき
もまた を法とする剰余系である.なぜならもし
を法とする剰余系である.なぜならもし
なら,  が
が と互いに素であることから
と互いに素であることから
となる.それは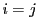 のときにかぎるからである.
ゆえに任意の
のときにかぎるからである.
ゆえに任意の に対して
に対して
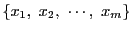 のなかのただ一つ
のなかのただ一つ
となる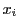 が存在する.
が存在する.
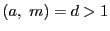 のとき.
のとき.
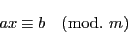 |
(2.3) |
に解があるとすると,
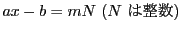 と表される.ゆえに
と表される.ゆえに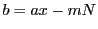 は
は
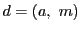 で割りきれる.そこで
で割りきれる.そこで
とおく.(2.3)は定理11 より
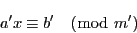 |
(2.4) |
と同値である.ここで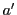 と
と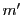 は互いに素であるから(2.4)を満たす
は互いに素であるから(2.4)を満たす は
は
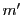 を法とする一つの類である.それを
を法とする一つの類である.それを
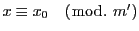 とする.
(2.4)の解は
とする.
(2.4)の解は
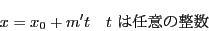 |
(2.5) |
によって与えられる.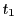 と
と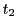 に対する
に対する が
が を法として合同になるのは
を法として合同になるのは
つまり
となるときにかぎる.
したがって,(2.5)で に対して,
に対して, を法とする剰余系
を法とする剰余系
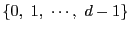 の値を与えるとき,
の値を与えるとき,  を法とする(2.3)のすべての解が得られる.すなわちその
解の個数は
を法とする(2.3)のすべての解が得られる.すなわちその
解の個数は である.□
である.□
このように合同方程式(2.3)を解くことは,一次不定方程式
の整数解を求めることと同じである.
定理 13
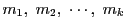
が二つずつ互いに素で,
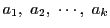
は
任意の整数であるとする.
を満たす

は
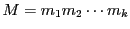
を法としてただ一つ存在する.■
証明
第一の合同式を満たす は
は
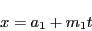 |
(2.7) |
と書ける.これが第二の合同式も満たすのは
すなわち
のときである.ところが, 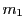 と
と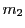 は互いに素なのでこれには
は互いに素なのでこれには
のように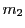 を法とするただ一つの類が解として存在する.これを(2.7)に代入して
を法とするただ一つの類が解として存在する.これを(2.7)に代入して
つまり
この一つの合同式を(2.6)の最初の二つの合同式に置き換えてよい.
同様の操作を繰りかえすことができる.ついには
を得る.□
この定理は 中国の剰余定理(Chinese Remainder Teorem) と呼ばれる.
中国古代(一世紀頃)の書『孫子算経』の中に,「3で割れば2余り,5で割れば3余り,
7で割れば2余るような数は何か」という問いと解の求め方が述べられている.
この種の問題が孫子以降の中国の算術の書に見られる.下って16世紀の終わり頃の
『算法統宗』(程大位)にはこの孫子の問いに対する解の求め方が歌で述べられている.
このような歴史があるのでこの定理が上のように呼ばれるのである.
ここでガウス(Gauss) による対称性を用いたより美しい別証を紹介する.
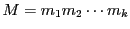 に対し
に対し
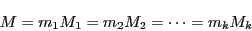 |
(2.8) |
とおく.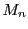 と
と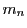 は互いに素なので
は互いに素なので
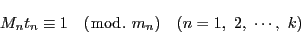 |
(2.9) |
となる解
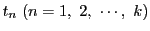 が存在する.
このとき(2.6)の解は
が存在する.
このとき(2.6)の解は
である.
実際,(2.9)から
で,
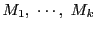 のうち
のうち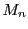 以外はすべて
以外はすべて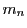 で割りきれるので,
で割りきれるので,
である.
唯一の解であることは, 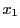 と
と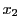 がともに(2.6)を満たせば
がともに(2.6)を満たせば
なので,
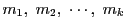 の最小公倍数
の最小公倍数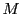 に関して
に関して
となるからである.□


 次: 合同方程式の解法
上: 合同式
前: 合同式
Aozora Gakuen
次: 合同方程式の解法
上: 合同式
前: 合同式
Aozora Gakuen
![]() を法とする剰余類のこととする.
合同方程式を解くとは,それを満たす剰余類を求めることとする.
簡単に「合同式を解く」ともいう.
を法とする剰余類のこととする.
合同方程式を解くとは,それを満たす剰余類を求めることとする.
簡単に「合同式を解く」ともいう.
![]() の
の![]() 個の値を代入してみればよい.つまりどんな合同方程式の解も,有限回の計算で求めることが出来る.
その意味で解を有理整数にかぎるなら,必ず解ける.
そのうえで,解の存在とより少ない手順で解を構成する方法を調べよう.
個の値を代入してみればよい.つまりどんな合同方程式の解も,有限回の計算で求めることが出来る.
その意味で解を有理整数にかぎるなら,必ず解ける.
そのうえで,解の存在とより少ない手順で解を構成する方法を調べよう.
![]() のとき.
のとき.
![]() は
は
![]() と
と![]() がともに(2.6)を満たせば
がともに(2.6)を満たせば