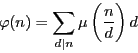次: 円順列への反転公式の応用
上: オイラーの関数
前: オイラーの関数
次: 円順列への反転公式の応用
上: オイラーの関数
前: オイラーの関数
一般に自然数で定義されたふたつの関数 $F(n),\ G(n)$ に対して,
関数等式
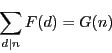 |
(2.23) |
が成り立つとき,これを逆に解いて $F(n)$ を $G(n)$を用いて表すことができる.
そのためにメビウス(Möbius)の関数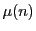 を次のように定義する.
を次のように定義する.
証明
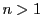 であるから
であるから  を素数のべきに因数分解して
を素数のべきに因数分解して
とする.よって
ここで和は
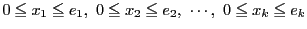 の範囲内のすべての
の範囲内のすべての
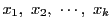 を動く.
この和の中で0になるもの,つまり各素数のべき指数が2以上のものを除くと,
を動く.
この和の中で0になるもの,つまり各素数のべき指数が2以上のものを除くと,
□
この 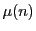 を用いると
を用いると 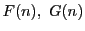 に関する問題を解くことができる.
に関する問題を解くことができる.
定理 20 (メビウスの反転公式)
整数で定義された二つの関数 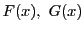 について二つの命題:
について二つの命題:
は同値である.■
証明
すべての  に対して第一式が成り立てば,それを第二式の右辺に代入して
に対して第一式が成り立てば,それを第二式の右辺に代入して
$\delta$ を固定し,$\delta|d|n$ であるように $d$ が動くと,
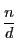 は
は
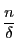 の約数全体を動く.
したがって和の順序を逆にして
の約数全体を動く.
したがって和の順序を逆にして
補題2 によってかっこ内の和で
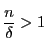 のものは0になり,
のものは0になり,
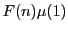 のみが残る.
のみが残る.
つぎにすべての  に対して第二式が成り立てば,同様に
に対して第二式が成り立てば,同様に
□
特に
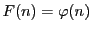 のときは
のときは 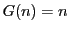 である.
この結果,整数で定義された関数で定理19の等式(2.22) がすべての
である.
この結果,整数で定義された関数で定理19の等式(2.22) がすべての  について成り立つものは
オイラーの関数
について成り立つものは
オイラーの関数 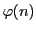 のみであることが示された.
そして
のみであることが示された.
そして
となる.こちらから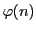 を計算する.
を計算する.
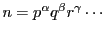 とすると
となり定理18と同じ結果が得られる.
とすると
となり定理18と同じ結果が得られる.


 次: 円順列への反転公式の応用
上: オイラーの関数
前: オイラーの関数
Aozora Gakuen
次: 円順列への反転公式の応用
上: オイラーの関数
前: オイラーの関数
Aozora Gakuen
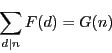
![]() を次のように定義する.
を次のように定義する.

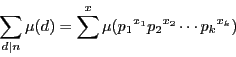
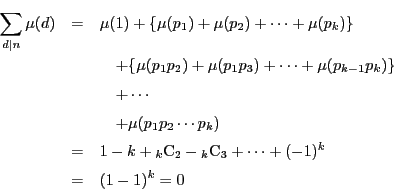
![]() を用いると
を用いると ![]() に関する問題を解くことができる.
に関する問題を解くことができる.
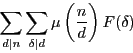
![]() は
は
![]() の約数全体を動く.
したがって和の順序を逆にして
の約数全体を動く.
したがって和の順序を逆にして
![\begin{displaymath}
=\sum_{\delta\vert n}\left[ F(\delta)\sum_{\delta'\vert \frac{n}{\delta}}\mu (\delta')\right]
\end{displaymath}](images/img935.gif)
![]() のものは0になり,
のものは0になり,
![]() のみが残る.
のみが残る.
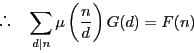
![]() に対して第二式が成り立てば,同様に
に対して第二式が成り立てば,同様に
![\begin{eqnarray*}
\sum_{d\vert n}F(d)
&=&\sum_{d\vert n}\sum_{\delta\vert d}...
...lta'\vert \frac{n}{\delta}}\mu(\delta')\right]
G(\delta)=G(n)
\end{eqnarray*}](images/img939.gif)
![]() のときは
のときは ![]() である.
この結果,整数で定義された関数で定理19の等式(2.22) がすべての
である.
この結果,整数で定義された関数で定理19の等式(2.22) がすべての ![]() について成り立つものは
オイラーの関数
について成り立つものは
オイラーの関数 ![]() のみであることが示された.
そして
のみであることが示された.
そして