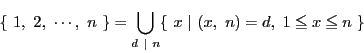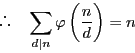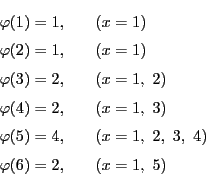
![]() をオイラーの関数という.
をオイラーの関数という.
![]() は自然数を定義域とする関数である.
は自然数を定義域とする関数である.
![]() が素数ならば,明らかに
が素数ならば,明らかに
![]() を法とする合同関係による商集合
を法とする合同関係による商集合![]() は
は
![]() 個の要素からなる集合であった.
個の要素からなる集合であった.
したがって「剰余類 ![]() が
が ![]() と互いに素である」ということが意味を持つ.
と互いに素である」ということが意味を持つ.
![]() と互いに素な剰余類
と互いに素な剰余類 ![]() を既約類という.またすべての既約類の
代表の一組を既約剰余系という.既約類は
を既約類という.またすべての既約類の
代表の一組を既約剰余系という.既約類は![]() 個ある.
個ある.
整数で定義された関数 ![]() が互いに素な二つの整数
が互いに素な二つの整数![]() と
と![]() に
対して
に
対して
証明
集合
さらにこれは既約類である.
なぜならもし ![]() が
が ![]() と互いに素でないとする.
と互いに素でないとする. ![]() と
と ![]() が互いに素なので
が互いに素なので
![]() または
または ![]() と互いに素でない.
と互いに素でない. ![]() と互いに素でないとする.
と互いに素でないとする.
ここで
![]() なる
なる ![]() をとると
をとると
つぎに ![]() を法とする任意の既約類
を法とする任意の既約類
![]() をとる.
をとる.
![]() と
と ![]() が互いに素なので
が互いに素なので ![]() となる
となる ![]() が存在する.
ゆえに既約類
が存在する.
ゆえに既約類
![]() は既約類
は既約類 ![]() と既約類
と既約類 ![]() から上の方法で作られる.
したがって
から上の方法で作られる.
したがって ![]() を法とする既約類
を法とする既約類
![]() と
と![]() を法とする既約類
を法とする既約類
![]() の一組と
の一組と
![]() を法とする既約類
を法とする既約類
![]() は一対一に対応する.
この組は
は一対一に対応する.
この組は
![]() 個あるので
個あるので![]() が示された□
が示された□
これが基本的な事実である.この証明は剰余類の定義にたちかえって行った. なお中国の剰余定理13を用いれば証明は簡明である.すなわち次のようになる.
別証明
いま
![]() および
および
![]() をそれぞれ
をそれぞれ ![]() と
と ![]() を法とする既約剰余系の一組とする.
を法とする既約剰余系の一組とする.
![]() 個の組合せの一つ
個の組合せの一つ
![]() に対して
に対して
逆に
![]() とすると,(2.20)となる
とすると,(2.20)となる
![]() が一意に決まる.
ゆえに
が一意に決まる.
ゆえに ![]() を法とする既約代表の一組の各数
を法とする既約代表の一組の各数 ![]() と
と
![]() の組の
間に一対一の対応が成り立つ.したがって
の組の
間に一対一の対応が成り立つ.したがって![]() が示された.□
が示された.□
![]() は次の定理によって計算される.
は次の定理によって計算される.
証明 定理17から
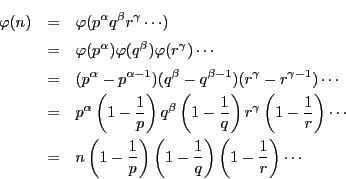
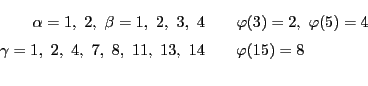

![]() は
は ![]() が
が ![]() を割り切ることを意味する記号であった.
を割り切ることを意味する記号であった.
![]() のときも
のときも![]() である.
である.
![]() と書けば,和は
と書けば,和は ![]() のすべての約数(1も
のすべての約数(1も ![]() も含む)にわたるものとする.
も含む)にわたるものとする.
証明
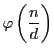 個ある.
個ある.
なぜなら
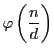 個である.
個である.
1から ![]() までの数
までの数 ![]() は
は ![]() の値が等しいものに分類できるので
の値が等しいものに分類できるので