

 次: 循環小数
上: フェルマの小定理
前: フェルマの小定理
次: 循環小数
上: フェルマの小定理
前: フェルマの小定理
定理 23 (オイラーの定理)

を正整数とし

を

と互いに素な整数とする.
このとき
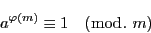 |
(2.29) |
が成り立つ.
とくに 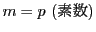 に対しては,
に対しては, 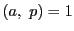 のとき
のとき
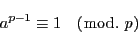 |
(2.30) |
が成り立つ.こちらの方を
フェルマの小定理という.■
証明
 を法とする既約類の個数は
を法とする既約類の個数は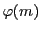 個ある.その一組を
個ある.その一組を
とする.このとき
もまた一組の既約剰余系である.
なぜなら 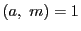 より
より
であるから  が剰余系なら
が剰余系なら 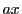 も剰余系である.
つまり
も剰余系である.
つまり  と
と  を法として合同な整数の集合とすれば,その集合の元にすべて
を法として合同な整数の集合とすれば,その集合の元にすべて  を乗じた
整数の集合は確かに
を乗じた
整数の集合は確かに 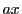 と合同な整数の全体になっており,
と合同な整数の全体になっており, 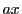 も剰余系である.
さらに
も剰余系である.
さらに  が
が  と互いに素なら
と互いに素なら 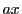 も
も  と互いに素なので,既約剰余系からは
既約剰余系が得られることもわかる.
と互いに素なので,既約剰余系からは
既約剰余系が得られることもわかる.
したがって二つの数の集合
の各元は  を法として互いに合同なものが一対一に対応している.
を法として互いに合同なものが一対一に対応している.
よって,その積は を法として互いに合同である.つまり
を法として互いに合同である.つまり
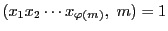 であるから
であるから
である.オイラーの定理(2.29)が示された.
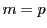 なら
なら
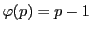 であるから,
オイラーの定理の特別な場合としてフェルマの小定理(2.30)が成り立つ.□
であるから,
オイラーの定理の特別な場合としてフェルマの小定理(2.30)が成り立つ.□
上の例で13の場合は4乗して初めて
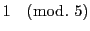 となるが,
11の場合は2乗した段階ですでに
となるが,
11の場合は2乗した段階ですでに
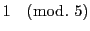 である.
である.
 のべきの中で
のべきの中で
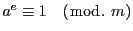 となる最小の
となる最小の 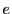 を
を
 の法
の法  に関する指数という.
に関する指数という.
定理 24

の法

に関する指数を
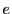
とする.
このとき
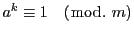
となったとすれば

は
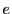
の倍数である.
特に
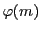
は
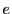
の倍数である.逆にいうと法

に関する指数となりうるのは
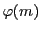
の約数にかぎる.■
証明
 を
を 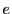 で割った商を
で割った商を  ,余りを
,余りを  とする.
とする.
ここで 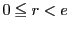 であるが,もし
であるが,もし 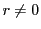 なら
なら
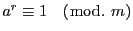 となる
正の整数
となる
正の整数  があることになり
があることになり 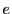 の最小性に反する.ゆえに
の最小性に反する.ゆえに 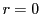 .
つまり
.
つまり  は
は 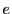 の倍数である.□
の倍数である.□


 次: 循環小数
上: フェルマの小定理
前: フェルマの小定理
Aozora Gakuen
次: 循環小数
上: フェルマの小定理
前: フェルマの小定理
Aozora Gakuen
![]() に対しては,
に対しては, ![]() のとき
のとき
![]() に対しては,
に対しては, ![]() のとき
のとき
![]() を法として互いに合同である.つまり
を法として互いに合同である.つまり
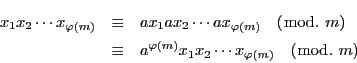
![]() なら
なら
![]() であるから,
オイラーの定理の特別な場合としてフェルマの小定理(2.30)が成り立つ.□
であるから,
オイラーの定理の特別な場合としてフェルマの小定理(2.30)が成り立つ.□
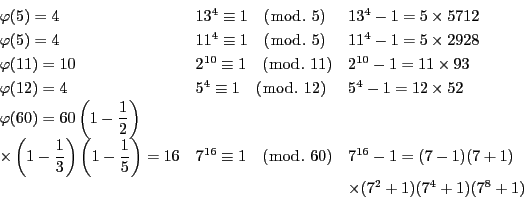
![]() となるが,
11の場合は2乗した段階ですでに
となるが,
11の場合は2乗した段階ですでに
![]() である.
である.
![]() のべきの中で
のべきの中で
![]() となる最小の
となる最小の ![]() を
を
![]() の法
の法 ![]() に関する指数という.
に関する指数という.
![]() を
を ![]() で割った商を
で割った商を ![]() ,余りを
,余りを ![]() とする.
とする.