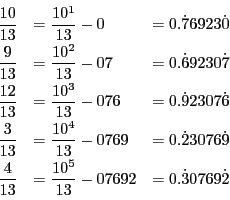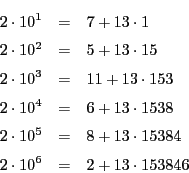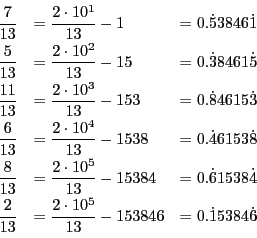となる最小の正整数である.
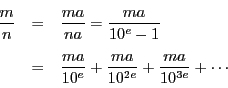
逆に![]() が
が ![]() 桁の循環節
桁の循環節 ![]() をもつ循環小数なら
をもつ循環小数なら
最小性は循環節の桁数の定義,つまりくりかえす最短の桁数,より明らか.□
![]() でないときはどうなるか.このとき
でないときはどうなるか.このとき ![]() とおく.
とおく.
![]() と
と ![]() の小さくない方を
の小さくない方を ![]() とする.
とする. ![]() .そして
.そして
![]() を約分して既約分数
を約分して既約分数
![]() を得るとする.
すると
を得るとする.
すると![]() である. 10の
である. 10の![]() を法とする指数を
を法とする指数を ![]() とすれば,
とすれば,
![]() は
は ![]() 桁の循環節をもつ循環小数になる.なお
桁の循環節をもつ循環小数になる.なお ![]() になればこれは有限小数である.
になればこれは有限小数である.
この定理は実例によって納得するのがよい.
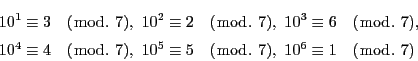
循環小数の作られ方を詳しく見てみよう.
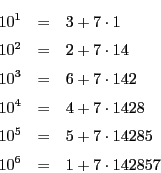
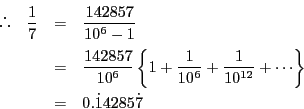
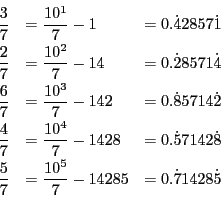
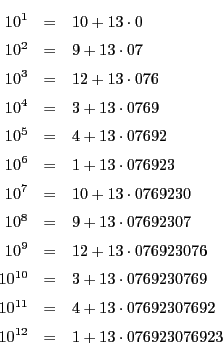
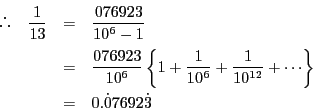
これから次の循環小数ができる.