次: 数学的帰納法 上: 自然数 前: 自然数

自然数の定義

自然数

「自然数」は，人が成長する過程で最初に習得する数である．3枚の皿に3個のみかんをひとつずつおいていけば，皿が余ったり，みかんが余ったりすることなくちょうど1枚の皿にみかんが1つずつおける．このような経験のなかから3枚の皿と3個のみかんは何かが「同じ」だと気づく．と，ここで実はこの一文ではすでに自然数「3」が用いられていることに気づく．

朝，小屋を出すとき，羊が通るたびに石を一つずつ置いていく．夕方帰ってきたときまたその石を羊が通るたびに動かす．最後の羊が通ったとき最後の石が動けば，迷子の羊がいないことがわかる．このとき朝の羊の何と夕べの羊な何が同じなのだろうと考えた．一対一の対応がつくとき，そこで何かが同じだ．一対一対応がつかないときは違う．同じとか違うとか一体何がと考え，同じものとしての「数」という概念が生まれていった．

また，数詞が生まれても，3個のみかんは3個のみかん，皿3枚は皿3枚と3が抽象されないまま用いられる膨大な時間があったにちがいない．そのときを経て，3が抽象されるとともに「数」の概念が生まれていった．

このように，個別のものの形や質などに規定された具体的な量から，個別の性質を捨て一般的な「数」を抽象する力を，人間は長い時間をかけて身につけた．数の発見は，実際はもっと生産に直結した場で起こったに違いない．毎朝放牧した羊と，夕べに帰ってきた羊が同じだけあるのかどうか，数を知らなければどのように判断するか．羊が小屋を出るたびに石をひとつ並べていく．帰ってきたときは，羊が小屋に入るたびに石をひとつ除く．こうしてちょうど最後の1頭が戻ったとき最後の石が除かれれば，増減がなかったことがわかる．石を並べることが長く続いた後，人は数を発見したのだ．あるいは実がなるまでに月の満ち欠けがどれだけくりかえされるか，こんなところにも数の発見の起源があるかも知れない．

人間が数をつかみ，それが親から子へと伝えられて，子供は成長のなかで数を身につける．大人からの伝達の作用によって，人類の長い歴史が凝縮されて，子供のなかで反復されるのだ．みかんのように数えられるものの個数がつかまれたなら，つぎは「水がバケツに3杯ある」などのように連続量をはかる単位が生まれ，単位の個数として水の量をつかむことができるようになったと考えられる．

このようにして見いだされた「自然数」は，数えるという行為と一体である．数えるという行為とは，このものを認識し，その次のものを確認して，自然数によって指示される抽象的な数との間に対応をつけていく，ということにある．最後に対応した数をその集合の要素の個数と認識する，ということである．このことを定式化して自然数を改めて数学の対象として定義しなおす．

自然数とは何か．

定義 1
$1$からはじめて,「1たす」という操作だけで作られる数の集合を自然数の集合といい，その要素を自然数という． ■

「だけで作られる」というところが大切である．つまり条件を満たす最小の集合である.「たす」という操作がどのようなものであるかは問わない．その操作を記号「＋」で表す．最初の対象「1」と操作「+」とその「くりかえし」，これだけである．1に1たした1+1を2と記し，2に1たした2+1を3と記し，以下順次命名してゆく．このように命名された要素の集合を$\mathbb{N}$と記す．その各要素を自然数という．

この定義から$\mathbb{N}$は次のような構造をもつことが示される．

(i)

(大小が定義される) 2つの自然数$a$と$b$は， $a$から始まって1たす操作を1回以上くりかえすことで$b$になるとき$a<b$と定め， $a$は$b$より小さい，$b$は$a$より大きいという．

(ii)

自然数の集合$\mathbb{N}$の部分集合には最小の要素がただ一つ存在する．

(iii)

(数学的帰納法の原理) $\mathbb{N}$の部分集合 $A$ が条件「$1 \in A$ ， かつ$x\in A$なら$x+1\in A$ 」 を満たすなら、$A$ は $\mathbb{N}$ 自身である．

これを証明するには，自然数の定義をもう少し厳密に定式化しなければならない．その作業はなかなか骨の折れることである．最終章「存在と構成」でその概略を示した．

最小要素の存在

自然数の性質(ii)は，要素が自然数からなる集合には最小の要素がただ一つ存在することを主張する．これは，整数分野の諸問題で存在証明の根拠になる．

一方，整数からなる集合や有理数からなる集合では最小要素があるとはかぎらない．例えば

$$\begin{eqnarray*} &&\{-5,\ -6,\ -7,\ \cdots\}=\{a\ \vert\ a は-5以下の整... ... =\left\{\dfrac{1}{2^k}\ \bigl\vert\ k は自然数\right\}\\ \end{eqnarray*}$$

などはいずれも最小の要素がない．

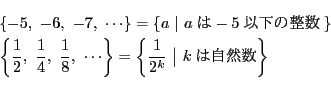
整数の部分集合でも，そのうち正の要素からなる部分集合には最小の要素が存在する．これを用いた存在証明の典型は一次不定方程式に解が存在することの証明である．

自然数の演算

自然数の集合$\mathbb{N}$の要素$a$と$b$には二つの演算，和$a+b$と積$ab$が定義される．定義されるとは$a$と$b$に対して$\mathbb{N}$の要素$a+b$と$ab$が一意に定まることを意味する．これを自然数の集合$\mathbb{N}$は加法と乗法で閉じているという．これに対して減法と除法については閉じていない．

$\mathbb{N}$を含み減法で閉じている最小の集合が整数の集合$\mathbb{Z}$であり， $\mathbb{N}$を含み除法で閉じている最小の集合が有理数の集合$\mathbb{Q}$である．

また整数$a$にはその絶対値 $\left\vert a \right\vert$が定義される．つまり

$$\left\vert a\right\vert=\left\{ \begin{array}{ll} a&(a \ge 0)\\ -a&(a < 0) \end{array} \right.$$

である．

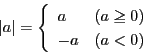
これらの演算の定義といくつかの演算法則の証明は，数学的帰納法による． それも最終章「存在と構成」でその概略を示した．