- 平方剰余の相互法則
:
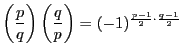
- 第一補充法則
:
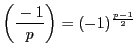
- 第二補充法則
:
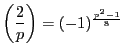
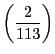 を求める一般的な方法はあるのか.
一般に
を求める一般的な方法はあるのか.
一般に
各法則の意味は次の通りである.
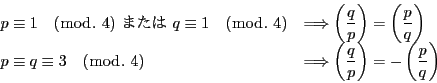
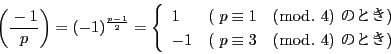
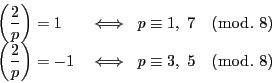
相互法則はすでにオイラー(Leonhard Euler,1707〜83)が多くの実例から帰納的に発見していた. ルジャンドル(Adrien Marie Legendre,1752〜1833)が定理 33 のような形式で表し, その証明を試みた. 彼はその証明の中で,初項と公差が互いに素な無限等差数列(算術級数)のなかに 素数が存在することを,証明なしに用いている.そのため証明は完全ではなかった.
相互法則を最初に完全に証明したのはガウス(Karl Friedrich Gauss,1777〜1855)である. ガウスは相互法則を整数論の基本法則と名づけ,なんと七つのまったく異なる証明を与えた. 「ガウスの予備定理」を用いるいちばん初等的な第三の証明法,および「ガウス和」を用いる 第四の証明法によって,証明する.