を
が成り立つ.■
証明
法 ![]() に関する剰余のうち
に関する剰余のうち ![]() より大きいものについて,
それから
より大きいものについて,
それから ![]() を引くと,絶対値において
を引くと,絶対値において ![]() より小さい剰余を得る.
より小さい剰余を得る.
![]() を法とする剰余をこのように絶対値で最小になるようにとると,
を法とする剰余をこのように絶対値で最小になるようにとると,
![]() はそのうち負な剰余の個数である.
(3.5)の数の絶対値最小な剰余は
はそのうち負な剰余の個数である.
(3.5)の数の絶対値最小な剰余は
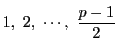 と一対一に対応し,そのうち
と一対一に対応し,そのうち
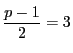 である.
である.
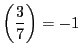 .
実際,法7に関する平方剰余は
.
実際,法7に関する平方剰余は 定理33のガウスによる第三証明
先に二つの補充則を示さなければならない.
第一補充則の証明.
オイラーの規準を ![]() で用いると得られる.
で用いると得られる.
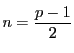
ガウスの予備定理を ![]() で用いる.(3.5)の数は
で用いる.(3.5)の数は
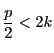 は
は
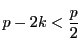 と同値であるから,
その個数は
と同値であるから,
その個数は
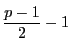 までである.いずれにせよ,
までである.いずれにせよ,
相互法則の証明.
![]() 平面上に点
平面上に点
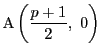 と
と
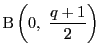 をとり点
をとり点
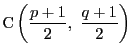 とする.
とする.
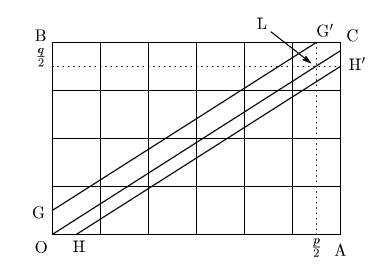
直線
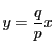 を引く.点
を引く.点
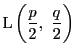 とする.
とする.![]() の内部で直線
の内部で直線![]() 上に格子点はない.
さて,
上に格子点はない.
さて,
 として,
として, ![]() を
を ![]() で割った絶対値最小剰余を
で割った絶対値最小剰余を
![]() とする.直線
とする.直線 ![]() と直線
と直線 ![]() の交点が
の交点が
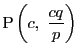 で,
で,
![]() は
直線
は
直線 ![]() 上の格子点で
上の格子点で![]() にもっとも近いものとの距離になり.
この格子点が
にもっとも近いものとの距離になり.
この格子点が ![]() より上にあるとき
より上にあるとき ![]() は負である.
は負である.
ガウスの予備定理を ![]() で考えると,そこにおける
で考えると,そこにおける ![]() は各
は各 ![]() に対して
直線
に対して
直線 ![]() 上
上
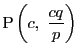 より上にあり,距離が
より上にあり,距離が ![]() より小さい格子点の個数である.
いま直線
より小さい格子点の個数である.
いま直線 ![]() を
を ![]() 軸の正の方向に
軸の正の方向に ![]() だけ平行移動した直線を
だけ平行移動した直線を
![]() する.
する. ![]() は平行四辺形
は平行四辺形
![]() の内部にある格子点の個数である.
の内部にある格子点の個数である.
同様にガウスの予備定理で
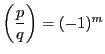 となる
となる ![]() は
直線
は
直線 ![]() を
を ![]() 軸の正の方向に
軸の正の方向に![]() だけ平行移動した直線を
だけ平行移動した直線を
![]() とするとき,平行四辺形
とするとき,平行四辺形
![]() の内部にある格子点の個数である.
の内部にある格子点の個数である.
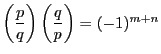 における
における ![]() は
この二つの平行四辺形の内部にある格子点の個数である.小四角形
は
この二つの平行四辺形の内部にある格子点の個数である.小四角形
![]() を付け加えて
六角形
を付け加えて
六角形
![]() の内部の格子点の個数もやはり
の内部の格子点の個数もやはり![]() である.
六角形
である.
六角形
![]() は
は ![]() の中点
の中点
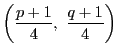 を対象の中心として点対称である.
したがって六角形
を対象の中心として点対称である.
したがって六角形
![]() 内の格子点は
内の格子点は
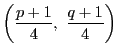 が格子点であるときはこれを除いて
その他の格子点は対象の中心に関して二つずつ組になっている.
が格子点であるときはこれを除いて
その他の格子点は対象の中心に関して二つずつ組になっている.
したがって ![]() が奇数であるか偶数であるかは,
点
が奇数であるか偶数であるかは,
点
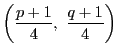 自身が格子点であるかないかによって決まる.
つまり
自身が格子点であるかないかによって決まる.
つまり![]() が奇数であるのは,
が奇数であるのは,
![]() ,
,
![]() がともに整数
がともに整数 ![]() となるときにかぎる.
となるときにかぎる.
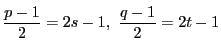 なので,これは
なので,これは
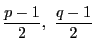 がともに奇数になることと同値である.
がともに奇数になることと同値である.
これで相互法則が証明された.□
相互法則その他を活用して ![]() と
と ![]() が与えられたとき,
が与えられたとき,
![]() の値を計算することができる.
の値を計算することができる.
