整数係数で考えるときはまた別の問題であることには注意したい.
![]() の多項式
の多項式![]() に対して
に対して![]() でその次数を表すとする.
でその次数を表すとする.
![]() の大きさをその次数
の大きさをその次数![]() とすると,
この大きさに対して除法の定理が成り立つ.
とすると,
この大きさに対して除法の定理が成り立つ.
証明
![]() のとき,
のとき,
![]() とする.
とする. ![]() と
と ![]() の
の ![]() 次の項をそれぞれ
次の項をそれぞれ
![]() とする.
とする.
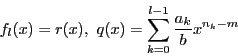
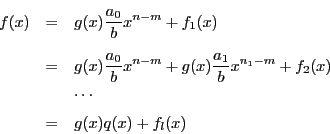
これが一組しかないことを示す.二組あったとする.
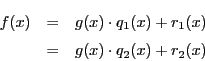
ところが一方,
![]() だから,
だから,
![]() .これは矛盾.
.これは矛盾.
ゆえに等式(4.1)が成立するのは,
![]() のときのみである.
このとき,
のときのみである.
このとき,
![]() となる.□
となる.□
多項式の場合も割り算ができ,
![]() を
を![]() に対して,
に対して,![]() を
を![]() で割った商と余りが一意に確定することから,
で割った商と余りが一意に確定することから,
が
の倍数であることは,
を
で割った余りが0であることと同値である.
因数分解は
![]() の中で,0でない定数は逆数もまた多項式であるから,
の中で,0でない定数は逆数もまた多項式であるから,
![]() では0でない定数が単数になる.
では0でない定数が単数になる.
既約かどうかは,定数倍しても変わらない.
ここで注意. 既約かどうかは,係数をどこで考えるかによって異なる.
公約数や公倍数は整数の場合と同じである.
2つの多項式![]() と
と![]() に対し,その最大公約数とは,
に対し,その最大公約数とは,
![]() と
と![]() の公約数のなかで次数が最も大きいものをいう.
最大公約数が定数のとき,
の公約数のなかで次数が最も大きいものをいう.
最大公約数が定数のとき,![]() と
と![]() は互いに素であるという.
は互いに素であるという.
最小公倍数とは,![]() と
と![]() の公倍数のなかで,
次数が最も小さいものをいう.
簡単のために,
の公倍数のなかで,
次数が最も小さいものをいう.
簡単のために,![]() や
や![]() などで多項式を表すことにする.
などで多項式を表すことにする.
整数の場合の証明が,ほんの一部の手直しでそのまま使える. ここでは(1)を示す.
証明
![]() の最小公倍数を
の最小公倍数を
![]() とし,
とし, ![]() を任意の公倍数とする.
を任意の公倍数とする.
![]() を
を ![]() で割った商を
で割った商を ![]() ,余りを
,余りを ![]() とすると
とすると
この定理の証明においても, 「除法の定理」が基本定理として用いられてることがわかる.
![]() は異なる既約な多項式,
は異なる既約な多項式,
![]() は正の整数である.
は正の整数である.
このとき整数と同様に次の定理が成り立つ.
多項式の場合も素因数分解の一意性という. 基本的な定理である.
整数の因数分解の一意性の証明にならって, 多項式の場合についても,除法を用いないツェルメロの方法による別証明をしてみよう.
因数分解の一意性の別証明
相異なる因数分解をもつ多項式が存在するとする.
異なる因数分解をもつ多項式の集合を考える.
この集合に属する次数が最小の多項式を![]() とする.
次数の集合は自然数の部分集合なので,最小値が存在する.
とする.
次数の集合は自然数の部分集合なので,最小値が存在する.
![]() は相異なる2つの因数分解をもつ.それを
は相異なる2つの因数分解をもつ.それを
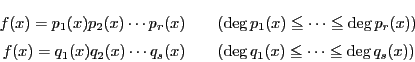
また,
![]() のいずれも
のいずれも
![]() のいずれとも異なる.
なぜなら,もし
のいずれとも異なる.
なぜなら,もし![]() なら,
これを約せば
なら,
これを約せば![]() より小さい次数で,異なる因数分解をもつ多項式が得られ,
より小さい次数で,異なる因数分解をもつ多項式が得られ,
![]() がそのような多項式のなかで次数最小であることに反する.
がそのような多項式のなかで次数最小であることに反する.
![]() とする.
とする.
![]() とすると,
適当な定数
とすると,
適当な定数![]() を
を
ここで多項式![]() を
を
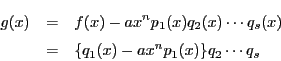
この![]() の因数分解における因数
の因数分解における因数
![]() は
は![]() の倍数ではない.
なぜならもし
の倍数ではない.
なぜならもし![]() の倍数なら
の倍数なら![]() が
が![]() の倍数となり,
互いに異なる既約な多項式であることに反する.
よってこの因数分解に
の倍数となり,
互いに異なる既約な多項式であることに反する.
よってこの因数分解に![]() は現れない.
は現れない.
一方![]() は
は
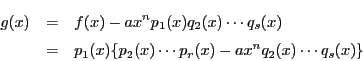
よって![]() の2つの因数分解は相異なる因数分解である.
の2つの因数分解は相異なる因数分解である.
![]() なので,
なので,
![]() が異なる2つの因数分解をもつ次数最小の多項式であることと矛盾した.
したがって異なる2つの因数分解をもつ多項式は存在しない.□
が異なる2つの因数分解をもつ次数最小の多項式であることと矛盾した.
したがって異なる2つの因数分解をもつ多項式は存在しない.□