

 次: ガウス整数環
上: 多項式環
前: 多項式の除法
次: ガウス整数環
上: 多項式環
前: 多項式の除法
一次不定方程式が多項式環でも考えられる.
そのために,整数の場合と同様に,
証明に除法が使われる基本定理を紹介しよう.
定理 40
![$K[x]$](images/img1575.gif)
の部分集合
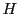
が空でなく
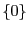
のみでもなく,
次の性質をもつとする.
このとき集合
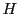
はある多項式
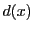
の倍数の全体と一致する.
つまり
である.■
証明
条件から
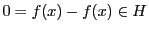 である.
その結果,
である.
その結果,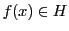 なら
なら
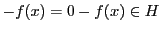 である.
そこで
である.
そこで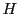 の要素のうち,
次数最小の多項式
の要素のうち,
次数最小の多項式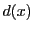 をとる.
をとる.
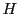 の任意の要素
の任意の要素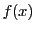 をとり,それを
をとり,それを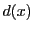 で割る.
で割る.
とおく.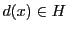 より
より
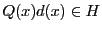 である.よって
である.よって
ここでもし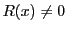 なら
なら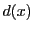 が次数最小の要素であることに反する.
よって
が次数最小の要素であることに反する.
よって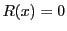 ,つまり
,つまり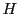 の任意の要素
の任意の要素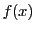 は
は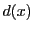 の倍数である.
したがって
の倍数である.
したがって
![$H=\{\ d(x)f(x)\ \vert\ f(x) \in K[x] \}$](images/img1665.gif) が示せた.□
が示せた.□
注意 4.2.1
整数環
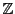
の場合は,差がふたたび属する部分集合

で考えた.この場合はこの条件から,
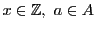
に対して
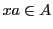
が導けた.しかし多項式環の場合は,別に条件として立てることが必要である.
一般に整域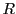 の部分集合
の部分集合 に対し,
に対し,
- (i)
 は加法に関して可換群である.
は加法に関して可換群である.
- (ii)
-
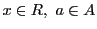 ならば
ならば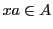 .
.
の二つが成り立つとき,

を
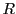
の
イデアルという.
整数環,多項式環ではイデアルはすべてある要素の倍数全体になる.このような整域を単項イデアル整域という.
定理40を用いると次のことが示される.
定理 41
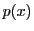
と
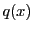
を互いに素な多項式とする.このとき
を満たす多項式
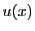
と
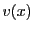
が存在する.
■
証明
とおく.
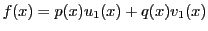 ,
,
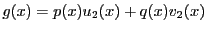 が
が
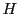 に属せば
に属せば
である.
したがって定理40より
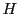 は,
は,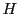 に属するある多項式
に属するある多項式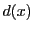 の倍数の全体である.
の倍数の全体である.
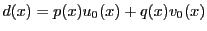 とする.
とする.
一方
なので,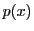 も
も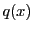 も
も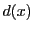 の倍数である.
つまり
の倍数である.
つまり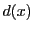 は
は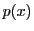 と
と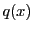 の公約数である.
の公約数である.
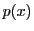 と
と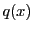 は互いに素なので,
は互いに素なので,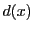 は定数である.
しかも,
は定数である.
しかも,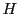 は0のみではないので
は0のみではないので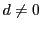 である.
である.
つまり
より
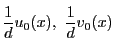 は
は
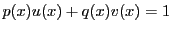 を満たす.□
を満たす.□
ユークリッドの互除法も同じようにできる.
簡単のために多項式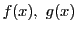 の最大公約数を
の最大公約数を 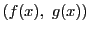 と書く.
と書く.
定理 42
- (1)
- 任意の多項式
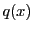 に対し,
に対し,
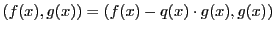 .
.
- (2)
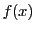 を
を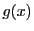 で割った余り
で割った余り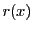 に対し,
に対し,
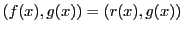 .
■
.
■
証明
(1)
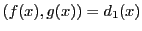 ,
,
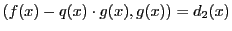 とする.
とする.
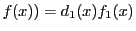 ,
,
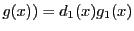 .また
.また
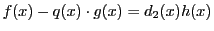 ,
,
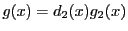 とする.
とする.
より
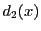 は
は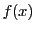 と
と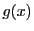 の公約数である.
の公約数である.
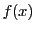 と
と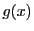 の最大公約数が
の最大公約数が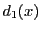 なので,
定理38(2)より,
なので,
定理38(2)より,
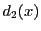 は
は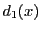 の約数である.
の約数である.
一方
より,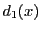 は
は
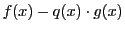 と
と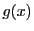 の公約数である.したがって同様の理由から
の公約数である.したがって同様の理由から
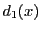 は
は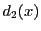 の約数である.
の約数である.
つまり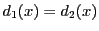 が示された.
が示された.
(2)
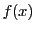 を
を 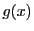 で割った商を
で割った商を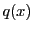 とすると,余りが
とすると,余りが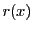 なので
なので
したがって,(1)から
となる.□
例 4.2.2
である.
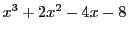
を
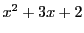
で割ることにより,
(2)から
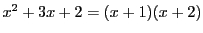
なので
注意 4.2.2
節末にいくつかの大学入試問題を紹介した.これらの入試問題は,多項式関数として解くこともでき,また多項式の整数論として解くこともできる.
整式は,一方で多項式関数として に値を代入し因数定理や剰余定理によって,式の除法や倍数や約数の議論をおこない因数分解の論証をすることができる.一方,有理数の一部である整数と同じように因数分解ができ,かつ素因数分解の(定数倍を除く)一意性が成り立つ.根拠はいずれも除法の基本性質なのであるが,証明の進め方はずいぶん異なる.
に値を代入し因数定理や剰余定理によって,式の除法や倍数や約数の議論をおこない因数分解の論証をすることができる.一方,有理数の一部である整数と同じように因数分解ができ,かつ素因数分解の(定数倍を除く)一意性が成り立つ.根拠はいずれも除法の基本性質なのであるが,証明の進め方はずいぶん異なる.
実際に二通りに解いてみてほしい.


 次: ガウス整数環
上: 多項式環
前: 多項式の除法
Aozora Gakuen
次: ガウス整数環
上: 多項式環
前: 多項式の除法
Aozora Gakuen
![\begin{eqnarray*}
&&f(x),\ g(x)\in H\quad \Rightarrow \quad f(x)-g(x)\in H\\
&&f(x)\in K[x],\ g(x)\in H\quad \Rightarrow \quad f(x)g(x)\in H
\end{eqnarray*}](images/img1654.gif)
![]() の任意の要素
の任意の要素![]() をとり,それを
をとり,それを![]() で割る.
で割る.
![]() なら
なら![]() が次数最小の要素であることに反する.
よって
が次数最小の要素であることに反する.
よって![]() ,つまり
,つまり![]() の任意の要素
の任意の要素![]() は
は![]() の倍数である.
したがって
の倍数である.
したがって
![]() が示せた.□
が示せた.□
![]() の部分集合
の部分集合![]() に対し,
に対し,
![]() ,
,
![]() が
が
![]() に属せば
に属せば
![]() は,
は,![]() に属するある多項式
に属するある多項式![]() の倍数の全体である.
の倍数の全体である.
![]() とする.
とする.
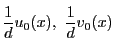 は
は
![]() ,
,
![]() とする.
とする.
![]() ,
,
![]() .また
.また
![]() ,
,
![]() とする.
とする.
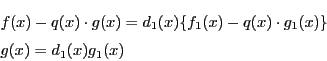
![]() が示された.
が示された.
![]() を
を ![]() で割った商を
で割った商を![]() とすると,余りが
とすると,余りが![]() なので
なので
![]() に値を代入し因数定理や剰余定理によって,式の除法や倍数や約数の議論をおこない因数分解の論証をすることができる.一方,有理数の一部である整数と同じように因数分解ができ,かつ素因数分解の(定数倍を除く)一意性が成り立つ.根拠はいずれも除法の基本性質なのであるが,証明の進め方はずいぶん異なる.
に値を代入し因数定理や剰余定理によって,式の除法や倍数や約数の議論をおこない因数分解の論証をすることができる.一方,有理数の一部である整数と同じように因数分解ができ,かつ素因数分解の(定数倍を除く)一意性が成り立つ.根拠はいずれも除法の基本性質なのであるが,証明の進め方はずいぶん異なる.