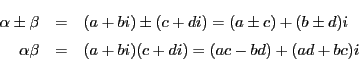
![]() の元
の元 ![]() に対して
に対して
![]() を
を ![]() の共役という.
これはふたたび整数で
の共役という.
これはふたたび整数で ![]() の元になる.
ここで
の元になる.
ここで![]() の元
の元 ![]() に対して
に対して
![]() の二つの元
の二つの元
![]() に対してその商
に対してその商
有理整数で逆数もまた整数になるのは ![]() と
と ![]() であった.
ガウス整数ではどのようなものになるだろうか.
であった.
ガウス整数ではどのようなものになるだろうか.
![]() は逆数
は逆数
![]() も整数であるとする.
このとき
も整数であるとする.
このとき
![]() が単数であるとき,
が単数であるとき, ![]() と
と ![]() を同伴数という.
を同伴数という.
![]() の同伴数は
の同伴数は
![]() である.
である.
二つの整数の割れる割れないの関係は,それらの整数を同伴数に置き換えて考えても
同じことになる.つまり整除の問題を考えるかぎり同伴数を同じ数のように考えて良い.
これは有理整数の整除の問題では![]() の因数を度外視して良く,多項式環では0でない定数倍の違いを度外視して良いのと同じである.
の因数を度外視して良く,多項式環では0でない定数倍の違いを度外視して良いのと同じである.
証明
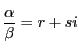 とおく.
ここに
とおく.
ここに ![]() は有理数である.
は有理数である.
この ![]() に対して整数
に対して整数 ![]() を
を
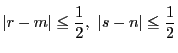 とることができる.
とることができる.
![]() とおく.
とおく.
このように除法の定理が成立する環をユークリッド整域というのだった.これで,整数環,整式環,ガウス環と三種のユークリッド整域を学んできたことになる. それらのカギになるのは,除法との関連で次のような「大きさ」が定義できたことであった.

証明
![]() の元のノルムの値の集合を考える.
それは0と自然数の部分集合であるからそのなかに0でない最小のものが存在する.
そのノルムを与える元を
の元のノルムの値の集合を考える.
それは0と自然数の部分集合であるからそのなかに0でない最小のものが存在する.
そのノルムを与える元を
![]() とする.
とする.
![]() の任意の元
の任意の元
![]() をとる.
をとる.
逆に![]() の倍数
の倍数
![]() が
が![]() に属することは明らかである.
に属することは明らかである.
また他の![]() もノルム最小の元なら,
もノルム最小の元なら,
![]() と
と![]() はノルムが等しいので単数倍違うのみである.□
はノルムが等しいので単数倍違うのみである.□
この![]() を
を ![]() と
と ![]() の最大公約数という.
ガウス環では除法を用いてユークリッドの互除法ができ
の最大公約数という.
ガウス環では除法を用いてユークリッドの互除法ができ
![]() と
と ![]() の最大公約数
の最大公約数![]() が単数倍の違いを除いて一意に存在することをが示された.
が単数倍の違いを除いて一意に存在することをが示された.
これによって整数環,多項式環の場合と同様に,ガウス環もまた単項イデアル整域である.