証明
異なる素因数分解をもつガウス整数の集合を考える.
この集合に属するノルム最小のガウス整数を![]() とする.
とする.
![]() は相異なる二つの因数分解をもつ.それを
は相異なる二つの因数分解をもつ.それを
また,
![]() のいずれも
のいずれも
![]() のいずれとも
同伴でない.なぜなら,もし
のいずれとも
同伴でない.なぜなら,もし![]() と
と![]() が同伴なら,
これを約せば
が同伴なら,
これを約せば![]() よりノルムが小さいガウス整数で,
異なる素因数分解をもつものが得られ,
よりノルムが小さいガウス整数で,
異なる素因数分解をもつものが得られ,
![]() がそのような数のなかでノルム最小であることに反する.
がそのような数のなかでノルム最小であることに反する.
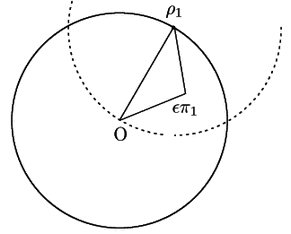
![]() とする.
とする.
![]() と同伴な4数
と同伴な4数![]() ,
,![]() ,
,![]() ,
,![]() のうちには,
のうちには,
![]() との偏角の差が
との偏角の差が
![]() 以下のものがある.
それを
以下のものがある.
それを![]() とする.
このとき,
とする.
このとき,
![]() が成り立つ.
が成り立つ.
ここでガウス整数![]() を
を
![]() の因数分解における因数
の因数分解における因数
![]() は
は![]() の倍数ではない.
なぜならもし
の倍数ではない.
なぜならもし![]() の倍数なら
の倍数なら![]() が
が![]() の倍数となり互いに異なる素数であることに反する.よってこの因数分解に
の倍数となり互いに異なる素数であることに反する.よってこの因数分解に![]() は現れない.
は現れない.
一方![]() は
は
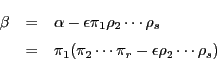
よって![]() の二つの因数分解は相異なる因数分解である.
の二つの因数分解は相異なる因数分解である.
![]() なので,
なので,
![]() が異なる二つの因数分解をもつ最小の自然数であることと矛盾した.
が異なる二つの因数分解をもつ最小の自然数であることと矛盾した.
したがって異なる二つの因数分解をもつ自然数は存在しない.□
ガウス環の素数はどのようなものか.
証明
![]() をガウス環
をガウス環 ![]() で因数分解しそれを
で因数分解しそれを
ノルムをとると
そうでなければ単数以外のノルムは ![]() であり,
であり, ![]()
![]() のとき
のとき ![]() と
と ![]() が同伴数なら
が同伴数なら![]() は
は
![]() のどれかと一致する.
のどれかと一致する.
![]() とすれば,
とすれば,![]() は虚数なので
は虚数なので
![]() はない.
はない.
![]() なら
なら![]() で,このとき
で,このとき![]() となり,
となり,
![]() なら
なら![]() で,このとき
で,このとき![]() となる.
しかし,
となる.
しかし,![]() は奇素数なのでこれらはあり得ない. □
は奇素数なのでこれらはあり得ない. □
![]() のとき,その分解は
のとき,その分解は
証明
一方が奇数で他方が偶数のとき,
![]() において
において![]() と
と![]() の偶奇が一致するので,
の偶奇が一致するので,
![]() が
が![]() で割り切れ,
で割り切れ,
![]() は
は![]() で割り切れない.
必要性が示せた.
□
で割り切れない.
必要性が示せた.
□
![]() で割り切れるか割り切れないかによって「偶数」,「奇数」
と読ぶ.ガウス整数の2での剰余類は
で割り切れるか割り切れないかによって「偶数」,「奇数」
と読ぶ.ガウス整数の2での剰余類は
証明 ガウス整数
では奇素数 ![]() がガウス環で分解されるか否かは何で決まるのか.
がガウス環で分解されるか否かは何で決まるのか.
証明
![]() がガウス素数のノルムであれば
がガウス素数のノルムであれば
![]() となる.
となる.
![]() が奇素数なので
が奇素数なので ![]() と
と ![]() の一方のみが偶数で他方が奇数になる.
の一方のみが偶数で他方が奇数になる.
したがって ![]() はガウス素数のノルムである.
はガウス素数のノルムである.
![]() のときの必要十分性が示されたので,
のときの必要十分性が示されたので,
![]() についての命題も成立する.
□
についての命題も成立する.
□
このことから「有理素数は,2か,または4を法として1に合同なときにかぎり,二つの平方数の和として一通りに書き表すことができる」ということがわかる.
本定理は平方剰余の第一補充法則を用いた.これを用いない初等的な大学入試問題がある.それを紹介しておきたい.2002年慶応大医学部問題(問題41)である.