

 次: 二次行列と実数の連分数展開
上: 連分数
前: 連分数
次: 二次行列と実数の連分数展開
上: 連分数
前: 連分数
定理6で,
一次不定方程式の解をユークリッドの互除法で構成するとき,
二次行列を用いると明快な表現ができることが示された.
そこで用いられたユークリッドの互除法を二次行列で表現する方法を再検討する.
 は0でないとする.整数
は0でないとする.整数 を
を で割って余りが
で割って余りが ,つまり
,つまり
であるとする.この除法の式は行列で
と表される.
ここで  と
と  の比を考えると,
の比を考えると,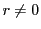 のとき
のとき
である.
ここに  は有理数
は有理数 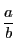 の整数部分であり,
の整数部分であり, 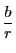 は小数部分の
逆数であることに注意しよう.
整数部分をとり,小数部分の逆数をとるという操作は,小数部分が0でないかぎり実行可能な操作である.この操作を行列で表現し,古典的な連分数との関連を調べることがこの節の目的である.
は小数部分の
逆数であることに注意しよう.
整数部分をとり,小数部分の逆数をとるという操作は,小数部分が0でないかぎり実行可能な操作である.この操作を行列で表現し,古典的な連分数との関連を調べることがこの節の目的である.
一般に,実数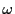 に対して,成分が実数の行列
に対して,成分が実数の行列
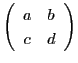 によって
実数
によって
実数
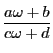 を対応させる変換をメービウス変換と呼び,
この実数を
を対応させる変換をメービウス変換と呼び,
この実数を
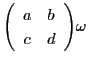 と記す.これは
と記す.これは
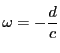 以外のすべての実数に対して定義される.
以外のすべての実数に対して定義される.
次のことはすぐに確認される.
-
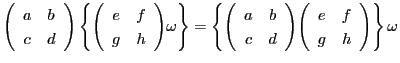
-
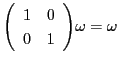
-
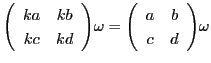
-
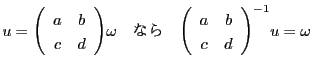
したがって,メービウス変換をくりかえし行った結果は,各行列の積の行列によるメービウス変換の結果と一致する.これをメービウス変換の積と呼ぶ.
実数の整数部分をとり,残された小数部分の逆数をとるという操作を繰り返すことが二次行列の積のメビウス変換で表される.
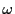 を整数でない正の実数とする.
また実数
を整数でない正の実数とする.
また実数 に対し
に対し![$[x]$](images/img1215.gif) は
は を越えない最大の整数を表す.
実数
を越えない最大の整数を表す.
実数 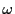 に対し,次の手続きを考える.
に対し,次の手続きを考える.
- (i)
![$q_0=[\omega]$](images/img1948.gif) とする.
とする.
- (ii)
-
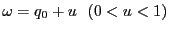 とおく.
とおく.
- (iii)
- そして
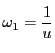 とする.
とする.
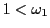 である.
である.
このとき,
と,上の手続きが二次行列で表現される.
数列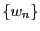 と数列
と数列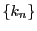 を,
を,
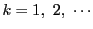 に対して
に対して
で定める.ただし,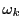 が整数となれば
いったんそこでやめるものとする.
が整数となれば
いったんそこでやめるものとする.
これを 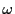 の 連分数展開という.
の 連分数展開という.
 回この手続きを行うと,
回この手続きを行うと,
となる.ここで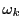 が整数になったとする.
そのときはそこで展開を終えるか,または次のようにもう一つ展開して終える.
が整数になったとする.
そのときはそこで展開を終えるか,または次のようにもう一つ展開して終える.
つまり,
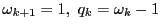 とする.
とする.
上の展開を「連分数展開」というのは,この手続きを一つの分数形式で書いていくと,次のようになるからである.
今後,連分数展開という表現で,行列の積としてメービウス変換の積を表すこともあれば,
分数形式で書いたものを表すこともある.
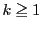 に対して
に対して
で 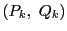 を定める.このとき
を定める.このとき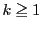 に対して,
に対して,
となる.
このような展開は本質的に一意である.
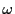 を整数でない実数とし,
を整数でない実数とし, 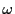 に二つの連分数展開ができたとする.
に二つの連分数展開ができたとする.
このとき,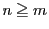 であれば,
であれば,
となる.
それを示すために,
と置く.
すると,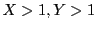 である.このとき,
である.このとき,
となり, 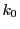 と
と 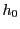 は同じ実数の整数部分であるから等しい.
この結果
は同じ実数の整数部分であるから等しい.
この結果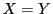 となる.同様の議論をくり返せば,順次
となる.同様の議論をくり返せば,順次
となるからである.
有理数の連分数展開は必ず有限で終わるが,その長さは,最後の展開の方法の調整によって
偶数,奇数のいずれのものも作ることができる.
ある数の連分数展開における違いは,この違いのみである.
また,有理数 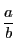 の連分数展開は,ユークリッドの互除法からつくったものと一致する.
つまり,互除法による展開が次のようになったとする.
の連分数展開は,ユークリッドの互除法からつくったものと一致する.
つまり,互除法による展開が次のようになったとする.
この途中をまとめ,
とおくと,
である.よって
となる.
つまり,
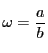 ,
,
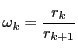 とおけば,
実数の連分数展開と一致する.
とおけば,
実数の連分数展開と一致する.


 次: 二次行列と実数の連分数展開
上: 連分数
前: 連分数
Aozora Gakuen
次: 二次行列と実数の連分数展開
上: 連分数
前: 連分数
Aozora Gakuen
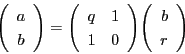
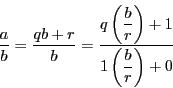
![]() に対して,成分が実数の行列
に対して,成分が実数の行列
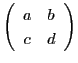 によって
実数
によって
実数
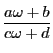 を対応させる変換をメービウス変換と呼び,
この実数を
を対応させる変換をメービウス変換と呼び,
この実数を
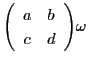 と記す.これは
と記す.これは
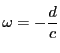 以外のすべての実数に対して定義される.
以外のすべての実数に対して定義される.
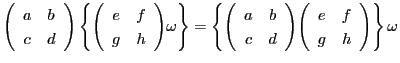
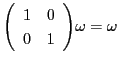
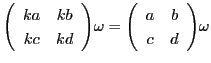
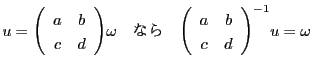
![]() を整数でない正の実数とする.
また実数
を整数でない正の実数とする.
また実数![]() に対し
に対し![]() は
は![]() を越えない最大の整数を表す.
実数
を越えない最大の整数を表す.
実数 ![]() に対し,次の手続きを考える.
に対し,次の手続きを考える.
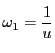 とする.
とする.
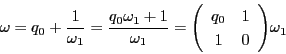
![]() と数列
と数列![]() を,
を,
![]() に対して
に対して
![\begin{displaymath}
\begin{array}{l}
\omega_0=\omega,\ q_0=[\omega],\ \\
...
...c{1}{\omega_{k-1}-q_{k-1}},\
q_k=[\omega_k]
\end{array}
\end{displaymath}](images/img1956.gif)
![]() の 連分数展開という.
の 連分数展開という.
![]() 回この手続きを行うと,
回この手続きを行うと,
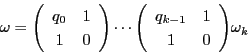
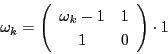
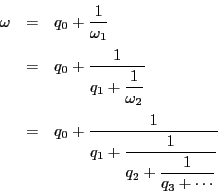
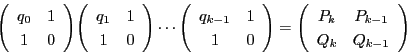
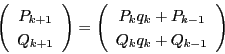
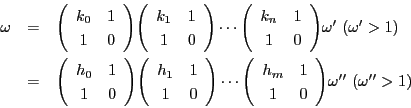
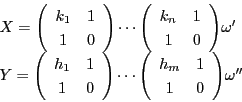
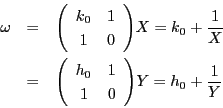
![]() の連分数展開は,ユークリッドの互除法からつくったものと一致する.
つまり,互除法による展開が次のようになったとする.
の連分数展開は,ユークリッドの互除法からつくったものと一致する.
つまり,互除法による展開が次のようになったとする.
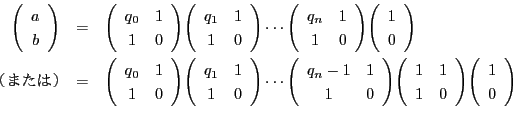
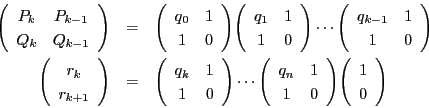
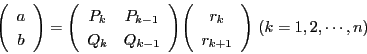
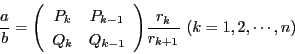
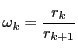 とおけば,
実数の連分数展開と一致する.
とおけば,
実数の連分数展開と一致する.