

 次: 連分数と格子点
上: 二次行列と実数の連分数展開
前: 最良近似分数
次: 連分数と格子点
上: 二次行列と実数の連分数展開
前: 最良近似分数
二つの実数 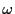 と
と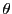 が,整数でかつ
が,整数でかつ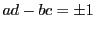 である
である 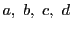 によって
によって
となっているとき, 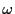 と
と 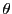 は 対等 であるという.
は 対等 であるという.
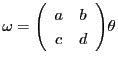 なら,
なら,
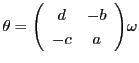 であるから,
一方が他方に対等であれば逆も対等である.対等もまた同値関係である.
であるから,
一方が他方に対等であれば逆も対等である.対等もまた同値関係である.
定理 51 (対等な無理数の基本性質)
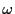
と
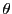
が対等な無理数で,
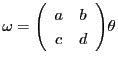
かつ,
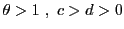
ならば,
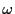
の連分数展開の途中に
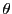
が現れる.
■
証明
とする,  と
と 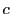 は互いに素なのでそのユークリッドの互除法を
は互いに素なのでそのユークリッドの互除法を
とする.
互いに素な整数の組の展開の個数  は偶数奇数いずれにもできるので,
は偶数奇数いずれにもできるので, 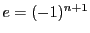 となる方の
となる方の  にしておく.
にしておく.
とおく.つまり
すると,
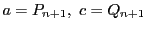 でさらに
でさらに
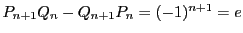 ,つまり
,つまり
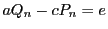 .
よって
.
よって 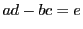 より,
より,
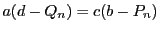 .
ところが
.
ところが  と
と 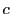 は互いに素であるから,
は互いに素であるから, 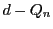 は
は 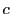 で割り切れる.
で割り切れる.
他方 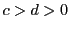 かつ
かつ
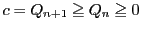 より,
より, 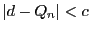 .
したがって
.
したがって 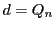 である.
その結果
である.
その結果 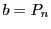 になる.
したがって,
になる.
したがって,
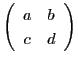 自身が
自身が
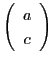 の展開を用いて
の展開を用いて
となる.つまり
となる.
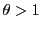 であるから,
展開の一意性より
であるから,
展開の一意性より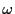 の連分数展開(の一部)そのものである.□
の連分数展開(の一部)そのものである.□
連分数展開の途中に現れる実数は,つねに対等であることに注意しよう.
例 5.2.1
連分数展開によって
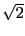
の近似分数列を求めよう.
こうして,
という近似分数列が得られる.
Aozora Gakuen
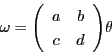
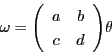
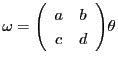 なら,
なら,
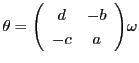 であるから,
一方が他方に対等であれば逆も対等である.対等もまた同値関係である.
であるから,
一方が他方に対等であれば逆も対等である.対等もまた同値関係である.
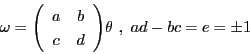
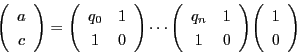
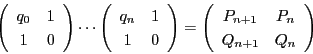
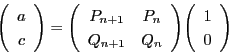
![]() かつ
かつ
![]() より,
より, ![]() .
したがって
.
したがって ![]() である.
その結果
である.
その結果 ![]() になる.
したがって,
になる.
したがって,
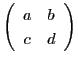 自身が
自身が
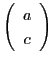 の展開を用いて
の展開を用いて
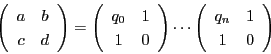
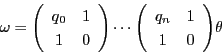
![]() であるから,
展開の一意性より
であるから,
展開の一意性より![]() の連分数展開(の一部)そのものである.□
の連分数展開(の一部)そのものである.□