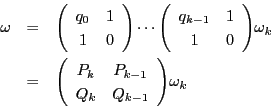
と置く.このとき,
-
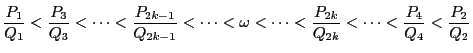
-
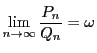
- 各
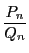 は既約である.
■
は既約である.
■
証明
数列
![]() の定義から
の定義から
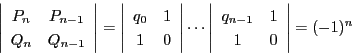
一方,
![]() より,
より,
![]() .
.
したがって
また,
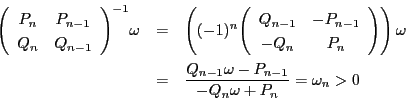
ここで
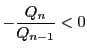 を乗じて
を乗じて
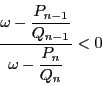
他方,明らかに
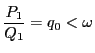 .よって
.よって
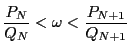 であるがさらに,
であるがさらに,
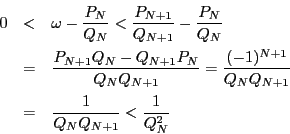
![]() を任意の偶数とする.同様に
を任意の偶数とする.同様に
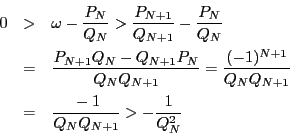
したがって
各
![]() のことを
のことを ![]() の 近似分数 という.
無理数
の 近似分数 という.
無理数 ![]() を近似する分数
を近似する分数 ![]() が,
が, ![]() なるどんな分数
なるどんな分数 ![]() に対しても
に対しても
証明 一般に正の数 ![]() に対し,
二つの分数
に対し,
二つの分数
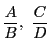 で
で ![]() であるものを考える.
このとき二つの分数は既約で,両分数の差は
であるものを考える.
このとき二つの分数は既約で,両分数の差は ![]() である.
である.
この二つの分数の間にある任意の分数 ![]() をとる.
をとる.
そこで
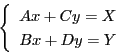
ここで分数 ![]() が
が
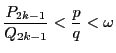 や
や
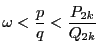 となる分数
となる分数
すなわち
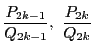 は最良近似分数である.
□
は最良近似分数である.
□
次の定理は「ペル方程式の解の存在」の定理58に対する別証明になっている.
ここで ![]() と
と ![]() の関係を定理58の逆にしている.
定理58では
の関係を定理58の逆にしている.
定理58では
![]() との関係で
との関係で ![]() を考えた.ここでは無理数
を考えた.ここでは無理数 ![]() を座標上の格子点
を座標上の格子点 ![]() で
で
![]() と近似することを考えるので
と近似することを考えるので ![]() を考察する.
を考察する.
定理58(再掲)
![]() が与えられた無理数とすると
が与えられた無理数とすると
証明
定理49の証明より,
すなわち,![]() は条件を満たす.
は条件を満たす.
![]() は無数に取ることができ,各近似分数は既約で
は無数に取ることができ,各近似分数は既約で ![]() は異なるので,
実際に無数の組が存在する.□
は異なるので,
実際に無数の組が存在する.□