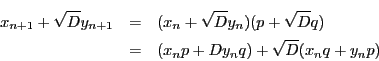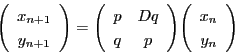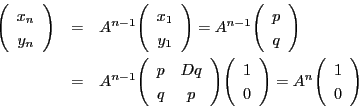次: ディリクレの原理
上: 解集合の構造と解の存在
前: 解集合の構造と解の存在
次: ディリクレの原理
上: 解集合の構造と解の存在
前: 解集合の構造と解の存在
二次不定方程式のなかで,
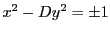 の形をしたものを「ペル方程式」という.
ここで,
の形をしたものを「ペル方程式」という.
ここで,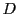 は平方数でない整数である.
この方程式の意義に気づき本格的に研究したのはフェルマである.本来は「フェルマ方程式」
と呼ぶべきだが,オイラーがある手紙の中で(不注意で)「ペル(J.Pell 1611-1685)方程式」と
呼んだために,今では「ペル方程式」が定着している.
は平方数でない整数である.
この方程式の意義に気づき本格的に研究したのはフェルマである.本来は「フェルマ方程式」
と呼ぶべきだが,オイラーがある手紙の中で(不注意で)「ペル(J.Pell 1611-1685)方程式」と
呼んだために,今では「ペル方程式」が定着している.
ペル方程式の場合も一次不定方程式の場合と同様,研究すべきは次の三項である.
- (i)
- ペル方程式の整数解の集合の構造
- (ii)
- ペル方程式に整数解が存在する証明
- (iii)
- ペル方程式の整数解を構成する方法
ちなみに『ペル方程式の解の構成』まで読み進めば 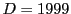 のとき,
のとき,
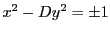 を満たす最小の正の整数解
を満たす最小の正の整数解 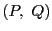 は
は
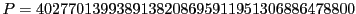
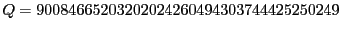
であることがわかる! これを楽しみにして進もう.
ところで,日本の大学の入学試験で「ペル方程式の整数解の集合の構造」に関する問題が過去何回か出題されている.高校生諸君の勉強の便宜を考え,材料としていくつかの入試問題を掘りさげるところから始めよう.まず,同じ95年に出題された二つの問題と85年の問題を解いてみよう.
例 6.1.1
[大阪府立大95年]
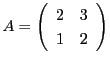 に対して,
に対して,
とする.次の問いに答えよ.
- (1)
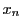 と
と 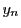 を求めよ.
を求めよ.
- (2)
-
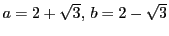 とおく.
とおく. 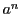 と
と 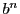 を
を 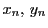 を用いて表せ.また,点
を用いて表せ.また,点
はすべて同じ曲線上にある. 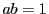 が成り立つことを利用して,
その曲線の方程式を求めよ.
が成り立つことを利用して,
その曲線の方程式を求めよ.
それぞれの解答をつける.
例6.1.1の解
- (1)
-
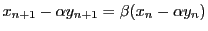 となる
となる
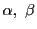 を求める.
を求める.
であるから,
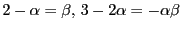 となり,
となり,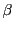 を
消去すると
を
消去すると 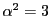 となり,
となり,
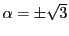 ,したがって
,したがって
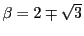 である.
つまり,
である.
つまり,
従って,
これを解いて,
- (2)
-
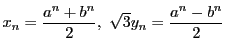 である.
両辺を二乗して辺々引くと
である.
両辺を二乗して辺々引くと
つまり
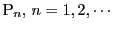 はすべて,曲線
はすべて,曲線 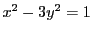 の上にある.
の上にある.
注意 6.1.1
ここでは手短に求めたが,
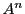
計算を行う方法がいくつか参考書には載っているので,
それから求めても良い.
つまり,一般に二次行列はハミルトン・ケイレイの定理によって,
となる実数

,

があるので,
となり,三項間漸化式と同じ方法で
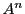
が求まる.
例6.1.2の解
- (1)
-
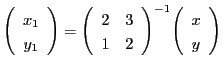 より
より
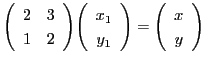 である.つまり,
である.つまり,
より,逆に解いて,
である.したがって,
- (2)
-
よって 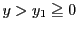 である.
である.
- (3)
- 府立大の問1と同様.ただし結果が与えられているので数学的帰納法で証明できる. ここでは数学的帰納法による証明をおこなおう.
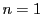 のときは,明らかである.
のときは,明らかである.
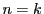 のとき,成立するとする.すなわち
のとき,成立するとする.すなわち
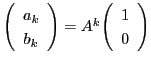 で定まる
で定まる 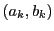 が
が
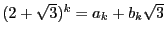 となるとする.
すると,
となるとする.
すると,
一方,
したがって, 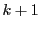 のときも成立する.
のときも成立する.
よってすべての自然数  に対して成立する.
に対して成立する.
- (4)
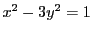 を満たす正の整数の組
を満たす正の整数の組 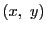 に対して,
に対して,
とおく.
すると(2)より 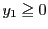 であるが,さらに
であるが,さらに
となるので, 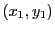 は
は 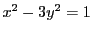 を満たす正の整数の組である.
を満たす正の整数の組である.
したがって,同じ操作を繰り返えすことができる.すなわち,順次
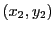 ,
, 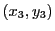 ,
, 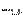 を定めることができる.このとき,
を定めることができる.このとき,
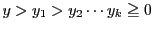 なので,ある番号
なので,ある番号  において
において 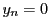 したがって
したがって 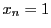 となる.すなわち
となる.すなわち
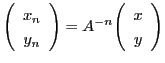 が
が
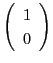 となる.
つまり
となる.
つまり
である.
□
例6.1.3の解
- (1)
- 求める
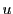 を
を
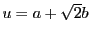 と置く.
と置く.
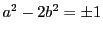 ,
つまり
,
つまり
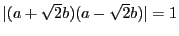 である.
である.
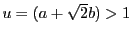 だから
だから
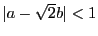 .
つまり
.
つまり
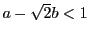 かつ
かつ
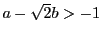 .
よって,
.
よって, 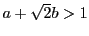 と辺々和と差をとることにより,
と辺々和と差をとることにより, 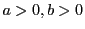 が得られる.
したがって最小となるのは
が得られる.
したがって最小となるのは 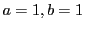 のときである.
のときである.
- (2)
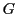 の任意の二元
の任意の二元 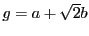 ,
,
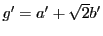 について,
について,
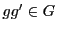 を示す.
を示す.
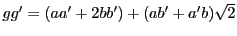 であるが,ここで,
であるが,ここで,
したがって, 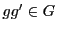 .
さらに,
.
さらに,
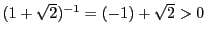 より,
より, 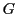 の元である.
その積はつねに
の元である.
その積はつねに 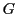 に属する.
に属する. 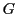 に属する元の積は再び
に属する元の積は再び 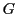 に属する.よって
すべての整数に対して
に属する.よって
すべての整数に対して 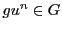 が示された.
が示された.
- (3)
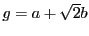 とする.
とする.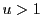 であるから
であるから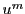 は
は が増加すれば増加する.
今
が増加すれば増加する.
今
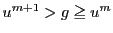 となる最大の
となる最大の  をとる.
したがって,
をとる.
したがって,
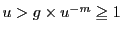 .
他方(2)と同様の考察により,
.
他方(2)と同様の考察により,
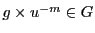 である.
したがって
である.
したがって 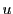 の最小性により,
の最小性により,
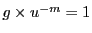 でなければならない.
すなわち,
でなければならない.
すなわち, 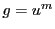 である.
□
である.
□
大阪府立大と明治大学の問題で記号の使い方が違うが,二つの集合を
とおくとき,大阪府立大の問題は,数列がペル方程式を満たすことを示せ,つまり
を示せといい,明治大の問題は,逆にそのペル方程式のすべての解がその数列から
得られることを示せ,つまり
を示せといっている.
必要条件と十分条件のそれぞれが同じ年に出題されたのである.
さらに,解の集合の構造がどのようになっているかについて,
観点を変えて出題したのが第三の東京工大の問題である.
ここには,この問題の本質的な解法が問われている.
東京工業大学の問題を一般化することでペル方程式の構造定理が得られる.
ペル方程式に 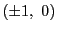 以外の解があることをこの節の最後に証明する.
まず,解に
以外の解があることをこの節の最後に証明する.
まず,解に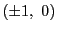 以外の解があるなら解の集合がどのようなものになるか,
これを定式化する.
1985年の東京工業大学の入試問題は,そのまま一般の場合の構造定理になる.
さらにあわせて,数列との関係もまとめたのが次の構造定理である.
以外の解があるなら解の集合がどのようなものになるか,
これを定式化する.
1985年の東京工業大学の入試問題は,そのまま一般の場合の構造定理になる.
さらにあわせて,数列との関係もまとめたのが次の構造定理である.
定理 57 (ペル方程式の解の構造定理)
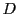
を平方数ではない正の整数とし,二次不定方程式
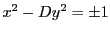
を考える.
解
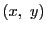
の部分集合
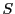
を次のように定める.
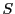
は
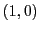
以外の解を持つとする.
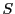 に属し,
に属し,
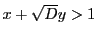 でかつ
でかつ 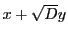 の値が最小となるものを
の値が最小となるものを
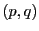 とする.
とする.
- (1)
-
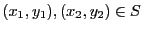 および任意の整数
および任意の整数  に対し,
に対し,
で 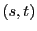 を定める.
を定める. 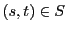 である.
である.
- (2)
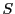 のすべての元は,整数
のすべての元は,整数  に対して,
に対して,
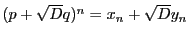 によって定まる
によって定まる 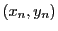 で得られる.
すなわち次式が成立する.ただし,
で得られる.
すなわち次式が成立する.ただし, 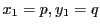 とする.
とする.
- (3)
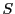 はまた行列
はまた行列
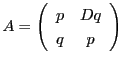 によって,
によって,
と書ける.
■
証明
- (1)
-
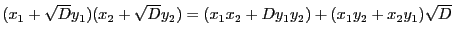
ここで,
よって,  のとき成立する.
のとき成立する.
次に, これより
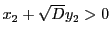 であるから,
であるから,
かつ,
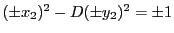 なので,
なので, 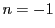 のときも成立し,
のときも成立し,
で定まる 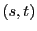 について,
について,
となった. そして,
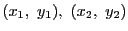 は任意であるから,
帰納的にすべての整数
は任意であるから,
帰納的にすべての整数  に対し成立する.
に対し成立する.
- (2)
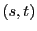 を
を 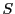 の元で,
の元で, 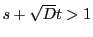 である任意の元とする.
である任意の元とする.
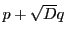 の最小性により,
の最小性により,
となる  が存在する. したがって,
が存在する. したがって,
ところが, (1)より
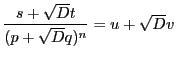 で定まる
で定まる 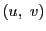 について,
について,
である. したがって, 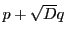 の最小性により,
の最小性により,
つまり, この場合ある  によって,
によって,
となった.
次に, 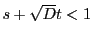 のとき,
のとき,
で, この
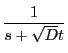 について,
について,
と表せば,
となり, この場合もある整数  によって,
によって,
となる.
逆に,
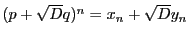 で定まる
で定まる 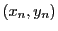 は, (1)
より
は, (1)
より  の元であるから, これで集合
の元であるから, これで集合 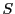 と集合
と集合
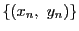 が一致す
ることが示された.
が一致す
ることが示された.
- (3)
-
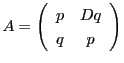 とする.
とする.
よって,
となる. したがって,
□


 次: ディリクレの原理
上: 解集合の構造と解の存在
前: 解集合の構造と解の存在
Aozora Gakuen
次: ディリクレの原理
上: 解集合の構造と解の存在
前: 解集合の構造と解の存在
Aozora Gakuen
![]() のとき,
のとき,
![]() を満たす最小の正の整数解
を満たす最小の正の整数解 ![]() は
は
![]()
![]()
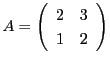 に対して,
に対して,
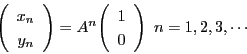
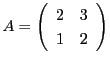 とする.以下の問いに答えよ.
とする.以下の問いに答えよ.
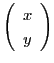 に対し,
に対し,
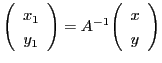 とおく.
とおく.
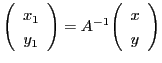 とおけば,
とおけば,
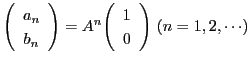 によって定めると,等式
によって定めると,等式
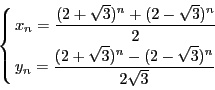
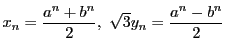 である.
両辺を二乗して辺々引くと
である.
両辺を二乗して辺々引くと
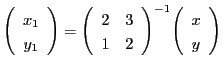 より
より
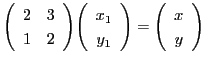 である.つまり,
である.つまり,
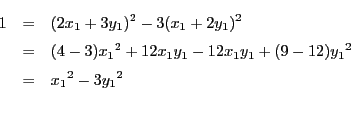
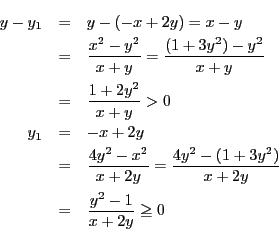
![]() のときは,明らかである.
のときは,明らかである.
![]() のとき,成立するとする.すなわち
のとき,成立するとする.すなわち
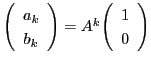 で定まる
で定まる ![]() が
が
![]() となるとする.
すると,
となるとする.
すると,
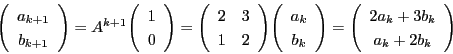
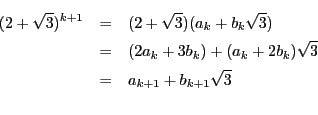
![]() に対して成立する.
に対して成立する.
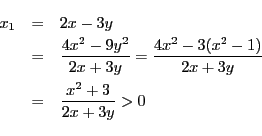
![]() ,
, ![]() ,
, ![]() を定めることができる.このとき,
を定めることができる.このとき,
![]() なので,ある番号
なので,ある番号 ![]() において
において ![]() したがって
したがって ![]() となる.すなわち
となる.すなわち
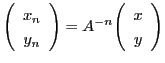 が
が
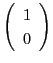 となる.
つまり
となる.
つまり
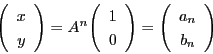
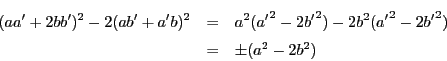
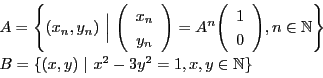
![]() に属し,
に属し,
![]() でかつ
でかつ ![]() の値が最小となるものを
の値が最小となるものを
![]() とする.
とする.
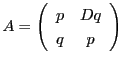 によって,
によって,
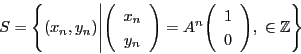
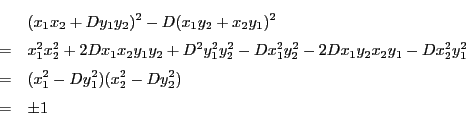
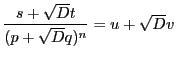 で定まる
で定まる ![]() のとき,
のとき,
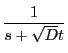 について,
について,
![]() で定まる
で定まる ![]() は, (1)
より
は, (1)
より ![]() の元であるから, これで集合
の元であるから, これで集合 ![]() と集合
と集合
![]() が一致す
ることが示された.
が一致す
ることが示された.
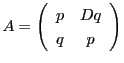 とする.
とする.