

 次: ペル方程式の解の存在
上: 解集合の構造と解の存在
前: ペル方程式の解の構造
次: ペル方程式の解の存在
上: 解集合の構造と解の存在
前: ペル方程式の解の構造
ペル方程式
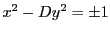 で解
で解 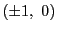 を「自明な解」という.
いつでも明らかに解になるからである.そこで以下でペル方程式に自明な解以外の
解が必ず存在することを証明する.
存在を保証するのは,ディリクレ(P.G.Dirichlet,1805-59)によって用いられた
まことに巧妙な「鳩の巣原理」と呼ばれる原理である.
を「自明な解」という.
いつでも明らかに解になるからである.そこで以下でペル方程式に自明な解以外の
解が必ず存在することを証明する.
存在を保証するのは,ディリクレ(P.G.Dirichlet,1805-59)によって用いられた
まことに巧妙な「鳩の巣原理」と呼ばれる原理である.
補題 8
- 自然数
 と
と に対し,
に対し, 人の人を
人の人を 個の部屋に入れることを考える.
個の部屋に入れることを考える.
 を
を で割った商を
で割った商を ,余りを
,余りを とおく.もし
とおく.もし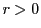 ならば,
少なくとも1つ,
ならば,
少なくとも1つ, 人より多くの人が入った部屋が存在する.
人より多くの人が入った部屋が存在する.
- 整数
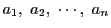 は,
すべて
は,
すべて
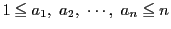 を満たし,
さらにすべて異なる.
このとき
を満たし,
さらにすべて異なる.
このとき
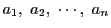 は
は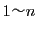 の値を一回ずつとる.
■
の値を一回ずつとる.
■
証明
- もしどの部屋も
 人以下なら,合計人数は
人以下なら,合計人数は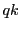 人以下になり
人以下になり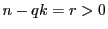 に反する.
ゆえに
に反する.
ゆえに 人より多くの人が入った部屋が存在する.
人より多くの人が入った部屋が存在する.
- もし
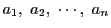 のなかに,
のなかに,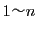 でとらない値があったとする.
その値を除く数を記した箱を用意する.箱の数は
でとらない値があったとする.
その値を除く数を記した箱を用意する.箱の数は 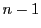 個以下になる.
数
個以下になる.
数
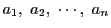 をその値にしたがってこれらの箱に入れる.鳩の巣原理によって
同じ箱に入るものが少なくとの一組できる.これは
をその値にしたがってこれらの箱に入れる.鳩の巣原理によって
同じ箱に入るものが少なくとの一組できる.これは
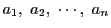 の値が
すべて異なることに矛盾する.
ゆえに
の値が
すべて異なることに矛盾する.
ゆえに
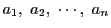 は
は の値を一回ずつとる.
□
の値を一回ずつとる.
□
この明快な原理によって次のディリクレによる定理が示され,
これをもとにペル方程式の解の存在が示される.
次の定理はすでに無理数の連分数展開を用いて
系54.1で示されているのであるが,
次のように直接に示すことができる.
定理 58
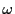
を与えられた無理数とする.このとき
となる整数
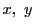
が
無数に 存在する.
■
証明
- 任意の自然数
 に対して,
に対して,
となる整数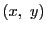 が少なくとも一組存在すること示す.
が少なくとも一組存在すること示す.
実数 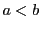 に対して
に対して  を含み
を含み  を含まない区間を
を含まない区間を
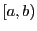 と表す.
区間
と表す.
区間 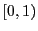 を次のように
を次のように  等分する.
等分する.
$ p $ に $ 0,1, \cdots , n $ の各値を与え,その $ p $ に対して,
$ \omega p $ を超えない最大の整数を $ q $ とする.
\[
0 \leqq \omega p-q < 1
\]
である.これらは全部で $ n+1 $ 個あるので,
鳩の巣原理によって上の $ n $ 個のうち少なくとも一つの区間には,
二つ以上の $ \omega p-q $ が属する.
$ \omega p_1-q_1 $ , $ \omega p_2 -q_2 $ ,
$ p_1\ne p_2 $ に対応する2つが同じ区間に属するとする.つまり
\[
|(\omega p_1-q_1)-(\omega p_2-q_2)| < \dfrac{1}{n}
\]
$ p_1 >p_2 $ とし, $ x=q_1-q_2,\ y=p_1-p_2 $ とおく.
この $ (x,\ y) $ に対して
\[
|\omega y-x| < \dfrac{1}{n}
\]
である.
- 各自然数
 に対して
に対して 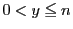 で
で
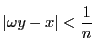 となる
となる 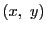 が
存在した.
が
存在した.
 を動かすとき,
これらの
を動かすとき,
これらの 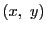 のなかに相異なるものが無数にあることを示す.
のなかに相異なるものが無数にあることを示す.
もし有限個しかなかったとする.
そのなかで 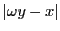 の値が最小のもの
を
の値が最小のもの
を
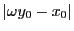 とする.それに対して,
とする.それに対して,
となる  をとる.
この
をとる.
この  に対して再び,
に対して再び,
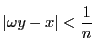 と
なるように
と
なるように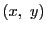 を選ぶことができる.ところが
を選ぶことができる.ところが
なので, 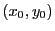 の最小性と矛盾した.
の最小性と矛盾した.
よって相異なるものは無数にある.
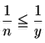 なので
なので
となる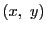 が無数にあることが示された.□
が無数にあることが示された.□


 次: ペル方程式の解の存在
上: 解集合の構造と解の存在
前: ペル方程式の解の構造
Aozora Gakuen
次: ペル方程式の解の存在
上: 解集合の構造と解の存在
前: ペル方程式の解の構造
Aozora Gakuen
 と
と に対し,
に対し, 人の人を
人の人を 個の部屋に入れることを考える.
個の部屋に入れることを考える.
 を
を で割った商を
で割った商を ,余りを
,余りを とおく.もし
とおく.もし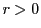 ならば,
少なくとも1つ,
ならば,
少なくとも1つ, 人より多くの人が入った部屋が存在する.
人より多くの人が入った部屋が存在する.
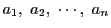 は,
すべて
は,
すべて
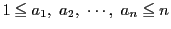 を満たし,
さらにすべて異なる.
このとき
を満たし,
さらにすべて異なる.
このとき
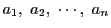 は
は の値を一回ずつとる.
■
の値を一回ずつとる.
■
![]() に対して
に対して ![]() を含み
を含み ![]() を含まない区間を
を含まない区間を
![]() と表す.
区間
と表す.
区間 ![]() を次のように
を次のように ![]() 等分する.
等分する.
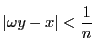 となる
となる ![]() の値が最小のもの
を
の値が最小のもの
を
![]() とする.それに対して,
とする.それに対して,
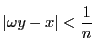 と
なるように
と
なるように![]() なので
なので