は,自明でない整数解
証明
定理58 により,
従って
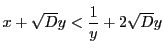 .
.
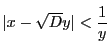 と乗じて,
と乗じて,
![]() は
は
![]() と
と
![]() の間にある(有限個の)整数の
うちのいくつかと一致する.
ところが
の間にある(有限個の)整数の
うちのいくつかと一致する.
ところが ![]() の組は無数のあるので少なくとも一つの整数
の組は無数のあるので少なくとも一つの整数 ![]() に対して,
に対して,
整数を ![]() で割った余りで分類すると,
で割った余りで分類すると, ![]() 組に分類される.整数の組
組に分類される.整数の組 ![]() は,
は,
![]() 個の有限個に分類される.他方
個の有限個に分類される.他方 ![]() は無数だから,分類されたどれかの組には無数
の
は無数だから,分類されたどれかの組には無数
の![]() が属する.
が属する.
![]() が同一の組に属するとする.
が同一の組に属するとする.
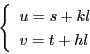
![]() である.
である. ![]() とおく.
とおく.
一方
![]() であるから,
であるから,
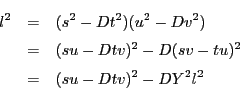
この定理によってペル方程式はつねに自明でない解をもち,
したがって前節の構造定理が空論ではないことが保証されるのである.