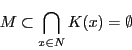次の性質を持つ集合
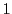 という要素がある.
という要素がある.
- 集合
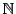 の要素
の要素 に対し集合
に対し集合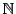 の要素
の要素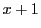 を対応させる規則が定まっている.
を対応させる規則が定まっている.
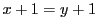 ならば
ならば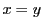 である.
である.
- 要素
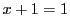 となる要素
となる要素  は存在しない.
は存在しない.
- 集合
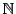 は(i)(ii)(iii)(iv)を満たす最小の集合である.
つまり
は(i)(ii)(iii)(iv)を満たす最小の集合である.
つまり 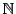 のどのような真部分集合も(i)(ii)(iii)(iv)を満たさない.
のどのような真部分集合も(i)(ii)(iii)(iv)を満たさない.
1と記号+と( )が組み合わさったものを要素とする集合
![]() を表記の簡単のために
を表記の簡単のために
この公理は,人間の「数える」という行為をそのまま定式化したものであるが,これが自然数論の基礎となるには色んな検証が必要である.数学基礎論では,この公理体系は矛盾が起こらないことが示されている.さらにこの公理はわれわれの自然数に対する素朴な理解と合致し,同型なものはひとつしかないことが示される.無矛盾性の証明は難しい.ここでは数学的帰納法の原理を含む自然数の基本性質がペアノの公理で構成された集合で成立することと,同型の意味を再確認したうえで自然数の体系はすべて同型であることを示そう.体系に矛盾がないことと,同じ型をしたものがただひとつであること,これで数学研究の対象が明確に定義できたのである.
(1) 1を含む任意の昇列 ![]() に対し,
に対し,
![]() において
において![]() に
に![]() を対応させる規則を
を対応させる規則を![]() に制限した規則を考える.
定義より,
に制限した規則を考える.
定義より,![]() のとき
のとき![]() であるから,
これは
であるから,
これは ![]() の要素
の要素 ![]() に
に ![]() を対応させる規則となる.
この対応の規則によって,
を対応させる規則となる.
この対応の規則によって, ![]() は 自然数の公理(i)(ii)(iii)(iv)を満たす.
は 自然数の公理(i)(ii)(iii)(iv)を満たす.
![]() の最小性から
の最小性から ![]() である.よってまた
である.よってまた ![]() を含む昇列はすべて
を含む昇列はすべて ![]() に一致する.
に一致する.
(2) ![]() は
は ![]() を含む昇列である.ゆえに(1)から
を含む昇列である.ゆえに(1)から ![]() .
.
(3) ![]() において,
において,
![]() にはじまり
にはじまり ![]() の操作を繰り返して
の操作を繰り返して ![]() に至る系列はただひとつである.
二つあれば,そのいずれかの系列を定めその中にのみ存在する要素を
に至る系列はただひとつである.
二つあれば,そのいずれかの系列を定めその中にのみ存在する要素を ![]() から取り除いても,
から取り除いても,
![]() は
は ![]() を含む昇列となり
を含む昇列となり ![]() の最小性に反するからである.
の最小性に反するからである.
![]() の要素
の要素 ![]() で
で ![]() でなく,
しかも
でなく,
しかも ![]() となる要素
となる要素 ![]() が存在しない要素の集合を
が存在しない要素の集合を ![]() とする.
とする.
次に ![]() かつ
かつ ![]() となるものがあるとする.二つの系列
となるものがあるとする.二つの系列
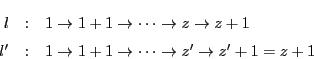
(4) ![]() なら
なら ![]() なので
なので![]() とする.
とする.
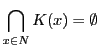 である.
つまり
である.
つまり