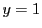 なら
なら 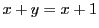 とする.
とする.
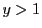 のとき.
のとき.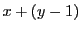 まで定まったとすると
まで定まったとすると
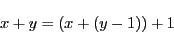
とする.
- (i)
- 結合法則:
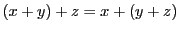 .
.
- (ii)
- 交換法則:
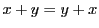 .
.
- (iii)
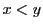 なら
なら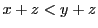 .
.
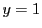 なら
なら 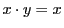 .
.
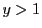 のとき.
のとき.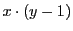 まで定まったとすると
まで定まったとすると
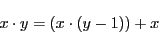
とする.
- (i)
- 結合法則:
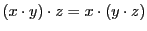 .
.
- (ii)
- 交換法則:
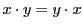 .
.
- (iii)
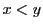 なら
なら
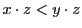 .
.
- (iv)
- 分配法則:
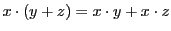 .
.
- (v)
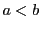 である任意の自然数に対し,
である任意の自然数に対し,
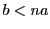 となる自然数
となる自然数 が存在する.■
が存在する.■
証明
これらの証明は,難しくはないが煩雑ではある.
例えば和の結合法則:
![]() を証明してみよう.
を証明してみよう.
数学的帰納法にもとづく和の定義より
![]() のとき.
のとき.
![]() は
は![]() と
と![]() の和の定義より成立する.
の和の定義より成立する.
![]() で成立するとする.
で成立するとする.
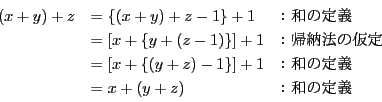
以下順次自然数と自然数の和・積が厳密に定義される.
また
![]() のとき,
のとき,
証明
![]() の
の ![]() への写像
への写像![]() を
を
![]() についての数学的帰納法で定める.
についての数学的帰納法で定める.
この
![]() を用いて
を用いて
![]() で
で![]() となるとする.
となるとする.