

 次: 解の発見法
上: 一次不定方程式
前: 差で閉じた部分集合
次: 解の発見法
上: 一次不定方程式
前: 差で閉じた部分集合
解の存在の証明には別の方法がある.その原理を説明する.
有限個のもののなかに,
ある条件を満たすものが存在することを示す根拠としてよく用いられるのが
鳩の巣原理とか部屋割り論法とかいわれる次の原理である.
同等な二つの形が用いられる.
- (i)
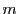 人を
人を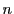 部屋に分けて入れる.
部屋に分けて入れる.
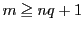 なら,
なら,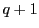 人以上入る部屋が存在する.
人以上入る部屋が存在する.
- (ii)
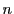 人を
人を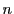 部屋に相部屋にならないように振り分ける.
各部屋に入るものが存在する.
部屋に相部屋にならないように振り分ける.
各部屋に入るものが存在する.
これを用いて定理7(2)の証明をしよう.
これは章末の演習問題14のように,入試問題でもよく出題される.
次の証明は演習問題14の(3),(4)と同じ内容である.
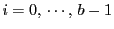 に対して
に対して 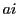 を
を 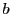 で割った余りを
で割った余りを 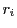 とする.
各
とする.
各 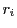 は0から
は0から 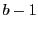 のどれかの値をとる.
のどれかの値をとる.
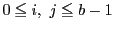 に対して
に対して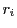 と
と 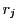 が
が 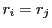 とする.
とする.
より
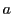 と
と 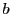 が互いに素なので
が互いに素なので 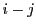 が
が 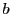 の倍数である.
の倍数である.
より,この範囲の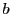 の倍数は,
の倍数は,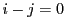 以外にない.
対偶をとると,
以外にない.
対偶をとると,
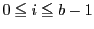 の
の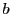 個の
個の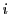 に対して,
同じ範囲の値
に対して,
同じ範囲の値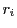 が対応し,これらのうちに同じ値がない.
鳩の巣原理によって
が対応し,これらのうちに同じ値がない.
鳩の巣原理によって
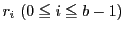 は0から
は0から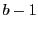 の各値を一つずつとる.
の各値を一つずつとる.
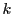 を
を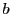 で割って商が
で割って商が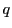 ,余りが
,余りが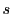 とする.
とする.
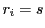 となる
となる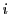 が存在する.
つまり
が存在する.
つまり
となる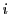 と
と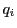 が存在する.
が存在する.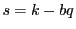 なので
なので
つまり
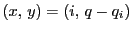 が
が 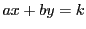 の解である.
(証明終わり)
演習問題14(2)は次のように一般的に成り立つ.
の解である.
(証明終わり)
演習問題14(2)は次のように一般的に成り立つ.
定理 8
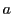
と
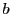
を互いに素な整数とし,不定方程式
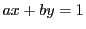
の1つの整数解を
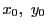
とする.
すべての整数解は次のように与えられる.
証明
任意の整数解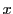 と
と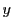 をとる.
をとる.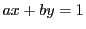 と
と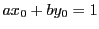 の辺々を引く.
の辺々を引く.
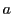 と
と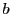 が互いに素なので,
が互いに素なので,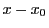 は
は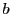 の倍数.これを
の倍数.これを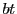 とおく.
このとき
とおく.
このとき
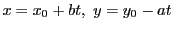 となる.
となる.
逆にある整数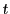 を用いてこの形に表される
を用いてこの形に表される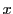 と
と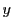 は不定方程式を満たす.
よって定理が示された.
(証明終わり)
は不定方程式を満たす.
よって定理が示された.
(証明終わり)
このよう一般的な形で表された解を一般解という.
これは,直線 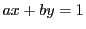 上には無数の格子点が等間隔に乗っていること,
それらを一般的な形に書くことができることを意味している.
上には無数の格子点が等間隔に乗っていること,
それらを一般的な形に書くことができることを意味している.
Aozora
2015-03-02
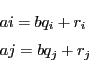
![]() を
を![]() で割って商が
で割って商が![]() ,余りが
,余りが![]() とする.
とする.
![]() となる
となる![]() が存在する.
つまり
が存在する.
つまり
![]() を用いてこの形に表される
を用いてこの形に表される![]() と
と![]() は不定方程式を満たす.
よって定理が示された.
(証明終わり)
は不定方程式を満たす.
よって定理が示された.
(証明終わり)
![]() 上には無数の格子点が等間隔に乗っていること,
それらを一般的な形に書くことができることを意味している.
上には無数の格子点が等間隔に乗っていること,
それらを一般的な形に書くことができることを意味している.