互いに異なる ![]() 個(
個(![]() )の実数の集合
)の実数の集合
![]() が次の性質をもつという.
が次の性質をもつという.
「このとき,から相異なる要素
,
をとれば
,
の少な くとも一方は必ず
に属する」
- (1)
- 次の2つのうちのいずれか一方が成り立つことを示せ.
(イ)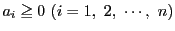
(ロ)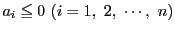
- (2)
-
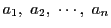 の順序を適当に変えれば
等差数列になることを示せ.
の順序を適当に変えれば
等差数列になることを示せ.
互いに異なる ![]() 個(
個(![]() )の実数の集合
)の実数の集合
![]() が次の性質をもつという.
が次の性質をもつという.
「このとき,から相異なる要素
,
をとれば
,
の少な くとも一方は必ず
に属する」
自然数を要素とする空集合でない集合![]() が次の条件(i),(ii)を満たしているとする.
が次の条件(i),(ii)を満たしているとする.
0以上の整数 ![]() に対して,
に対して, ![]() で
で ![]() の下3桁を表すことにする.
たとえば,
の下3桁を表すことにする.
たとえば,
![]() である.
である.![]() を2でも5でも割り切れない正の整数とする.
を2でも5でも割り切れない正の整数とする.
![]() は互いに素な正の整数とする.
は互いに素な正の整数とする.
![]() 平面上の点で
平面上の点で ![]() 座標,
座標, ![]() 座標がともに整数である点を格子点という.
座標がともに整数である点を格子点という.
![]() は整数で
は整数で ![]() とし,直線
とし,直線
![]() とおく.
自然数
とおく.
自然数![]() に対して,平面上の点
に対して,平面上の点![]() の集合
の集合