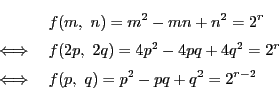- (1)
- (イ),(ロ)とも成り立たないとする.
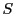 の属する最大の数を
の属する最大の数を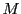 ,
最小の数を
,
最小の数を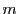 とする.
このとき
とする.
このとき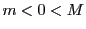 が成り立っている.
が成り立っている.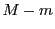 か
か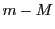 は
は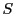 に属するので,
に属するので,
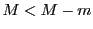 または
または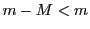 が成り立つ.
これは
が成り立つ.
これは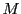 の最大性または
の最大性または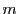 の最小性に矛盾する.
よって(イ),(ロ)のうちいずれか一方が成立する.
の最小性に矛盾する.
よって(イ),(ロ)のうちいずれか一方が成立する.
- (2)
- (イ)が成り立っているとする.
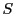 の要素で正で最小のものを
の要素で正で最小のものを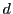 とする.
とする.
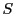 の
の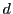 と異なる正の任意の要素
と異なる正の任意の要素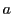 をとる.
をとる.
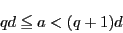
となる自然数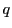 をとる.
をとる.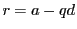 とおく.
とおく.
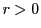 とする.
とする.
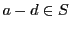 であり,自然数
であり,自然数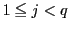 に対して
に対して
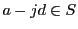 なら
なら
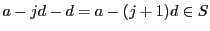 なので,数学的帰納法で
なので,数学的帰納法で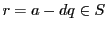 である.
である.
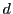 が
が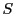 の要素で正で最小のものであるという仮定に反する.よって
の要素で正で最小のものであるという仮定に反する.よって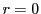 である.
である.
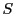 のすべての要素は
のすべての要素は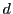 の倍数である.
の倍数である.
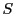 に属する最大の要素を
に属する最大の要素を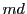 とおく,
とおく,
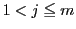 の整数に対して
の整数に対して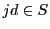 なら
なら
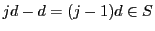 なので
なので
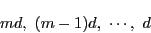
はすべて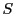 に属する.要素の個数は,
0が
に属する.要素の個数は,
0が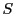 にあるかどうかを考え
にあるかどうかを考え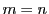 か
か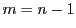 であり
であり
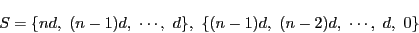
のいずれかである.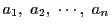 の順序を適当に変えれば
初項が
の順序を適当に変えれば
初項が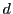 または0,公差
または0,公差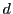 の等差数列になる.
の等差数列になる.
(ロ)の場合,すべての要素の絶対値をとって考えれば同様である.
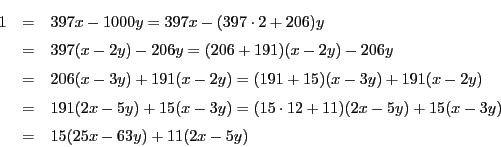
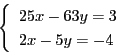
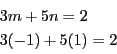
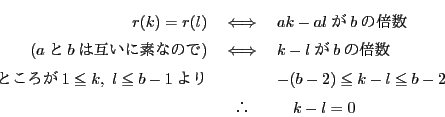
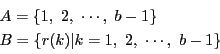
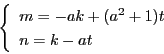
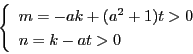

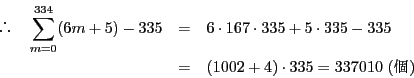
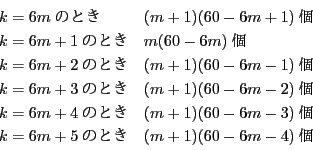
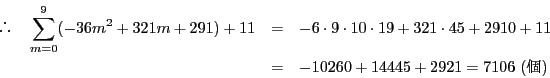
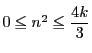 となり,
となり,
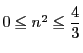 より
より
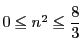 .この範囲の偶数は
.この範囲の偶数は