

 次: 剰余系
上: 余りによる類別
前: 余りによる類別
次: 剰余系
上: 余りによる類別
前: 余りによる類別
整数 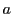 と
と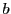 の差が
の差が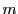 の倍数であるとき,
の倍数であるとき,
といい,次のように記す.
次のことは高校数学範囲では証明なしに用いてよい.
しかしまた,証明されることであることも知っておこう.
定理 9
2整数
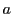
と
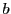
が
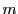
を法として合同であることと,
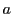
と
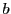
を
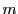
で割った二つの余りが等しいことは同値である.
証明
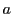 と
と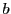 が
が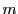 を法として合同であるとする.
を法として合同であるとする.
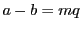 とおける.
とおける.
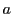 と
と 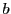 を
を 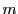 で割った商と余りをそれぞれ
で割った商と余りをそれぞれ 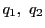 ,
,
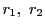 とする.
とする.
2式の辺々を引いて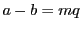 を用いると
を用いると
つまり
もし
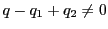 なら,
なら,
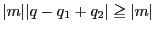 であるが,
右辺は
であるが,
右辺は 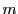 で割った余りの差なので
で割った余りの差なので 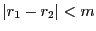 となり矛盾する.
となり矛盾する.
逆に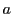 と
と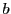 を
を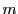 で割った余りが等しいとする.
で割った余りが等しいとする.
より
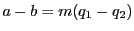 である.つまり
である.つまり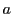 と
と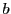 は
は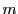 を法として合同である.
(証明終わり)
を法として合同である.
(証明終わり)
Aozora
2015-03-02
![]() と
と![]() が
が![]() を法として合同であるとする.
を法として合同であるとする.
![]() とおける.
とおける.
![]() と
と ![]() を
を ![]() で割った商と余りをそれぞれ
で割った商と余りをそれぞれ ![]() ,
,
![]() とする.
とする.
![]() と
と![]() を
を![]() で割った余りが等しいとする.
で割った余りが等しいとする.