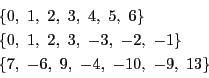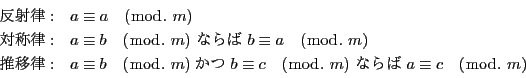
なぜうまく分けられるのだろうか.
合同であるという関係は,
等号や図形の相似や合同などと同じく,次の三つの規律に従う.
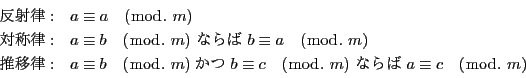
一つ一つの部分集合を![]() を法とする類,あるいは剰余類といい,
類に分けることを類別という.
を法とする類,あるいは剰余類といい,
類に分けることを類別という.
![]() を法とする類とは,
を法とする類とは, ![]() を法として互いに合同なすべての数の集合である.いいかえると
を法として互いに合同なすべての数の集合である.いいかえると![]() で割ったとき余りの等しい整数の集合である.よって
で割ったとき余りの等しい整数の集合である.よって![]() を法とする類別では
を法とする類別では![]() 個の類に類別される.
個の類に類別される.
各集合について,その集合に属する一つの要素 ![]() をとれば,同じ集合に属するすべての要素は,整数
をとれば,同じ集合に属するすべての要素は,整数![]() を用いて
を用いて![]() と表される.
と表される.
![]() を法として
を法として ![]() 個に分けられた各集合から一つずつ代表を取り出したとき,それを
完全な代表の一組(または剰余系)という.
例えば
個に分けられた各集合から一つずつ代表を取り出したとき,それを
完全な代表の一組(または剰余系)という.
例えば