

 次: 演習問題
上: 余りによる類別
前: 剰余系
次: 演習問題
上: 余りによる類別
前: 剰余系
合同であることを示す関係式
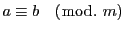 は,
整数の和差積に関して,等式の場合と同じく次のことが成り立つ.
は,
整数の和差積に関して,等式の場合と同じく次のことが成り立つ.
定理 10
以下,各文字は整数を表す.
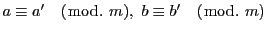 ならば
ならば
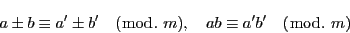 |
(1) |
である.一般に
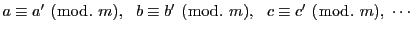
で
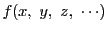
が
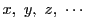
に関する整数係数の整式ならば
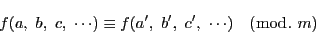 |
(2) |
証明
仮定によって
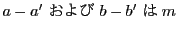 の倍数である.
ゆえに
の倍数である.
ゆえに
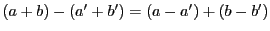 は
は 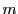 の倍数である.また,
の倍数である.また,
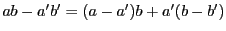 も
も 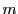 の倍数である.すなわち(1)が示された.
の倍数である.すなわち(1)が示された.
(1)から
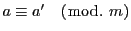 なら次のことが成り立つ.
なら次のことが成り立つ.
1) 任意の整数 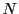 に対して
に対して
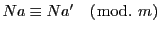 .
.
2) 数学的帰納法と組みあわせて自然数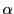 に対し
に対し
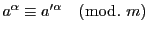 .
.
ふたたび(1)から
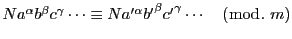 である.
である.
もういちど(1)から
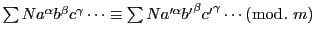 となり
(2)が示された.
(証明終わり)
となり
(2)が示された.
(証明終わり)
合同式に関する二つの定理を紹介する.
第一は数の等式での命題
に対応するものである.
定理 11
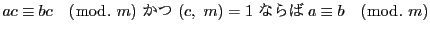
証明
仮定から 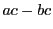 は
は 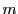 の倍数つまり整数
の倍数つまり整数 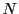 で
で
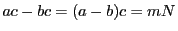 となるものがある.
となるものがある.
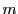 と
と 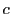 は互いに素なのでこれから
は互いに素なのでこれから 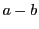 が
が 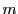 の倍数であることがわかる.つまり
の倍数であることがわかる.つまり
が示された.
(証明終わり)
第二は,逆数の存在に関するものである.
定理 12
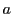
と
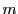
が互いに素なとき
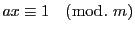
となる整数
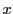
が存在する.
証明
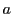 と
と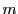 が互いに素なので,一次不定方程式
が互いに素なので,一次不定方程式
は整数解
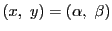 をもつ.
をもつ.
なので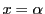 が条件を満たす整数である.
(証明終わり)
が条件を満たす整数である.
(証明終わり)
注意 2
ここは高校数学範囲を越えることであるが,定理
10の意味は,2つの剰余類からそれぞれそこに属する整数をとりだし,
その加法や乗法をおこなうと,その和や積の属する剰余類は,とりだした整数によらず確定する,ということである.この結果,剰余類の間に加法や乗法を定めることができる.
合同式(
1)は,このようにつかんではじめてその意味がわかる.
Aozora
2015-03-02
![]() ならば
ならば
![]() の倍数である.
ゆえに
の倍数である.
ゆえに
![]() は
は ![]() の倍数である.また,
の倍数である.また,
![]() も
も ![]() の倍数である.すなわち(1)が示された.
の倍数である.すなわち(1)が示された.
![]() なら次のことが成り立つ.
なら次のことが成り立つ.
![]() に対して
に対して
![]() .
.
![]() に対し
に対し
![]() .
.
![]() である.
である.
![]() となり
(2)が示された.
(証明終わり)
となり
(2)が示された.
(証明終わり)