次: 整数の約数と倍数 上: 自然数 前: 自然数とは

自然数の基本性質

この定義から自然数の集合$\mathbb{N}$は次のような性質をもつことが示される． これを証明するためには，自然数の定義をさらに厳密にしなければならない．それは略する． その意味を説明する．

(i) 大小関係

2つの自然数$a$と$b$は，$a$から始まって1たす操作をくりかえすことで$b$になるとき$a<b$と定め， $a$は$b$より小さい，$b$は$a$より大きいという．

異なる自然数$a$と$b$はつねに，いずれかが他方より大きく，比較がいつでもできる．

(ii) 最小要素の存在

自然数の集合$\mathbb{N}$の部分集合には最小の要素がただ一つ存在する．

要素が自然数からなる集合には最小の要素がただ一つ存在することを主張する． これは，整数分野の諸問題で存在証明の根拠になる．

一方，整数からなる集合や有理数からなる集合では最小要素があるとはかぎらない．例えば

$$\begin{eqnarray*} &&\{-5,\ -6,\ -7,\ \cdots\}=\{a\ \vert\ a は-5以下の整?... ... =\left\{\dfrac{1}{2^k}\ \bigl\vert\ k は自然数\right\}\\ \end{eqnarray*}$$

などはいずれも最小の要素がない．

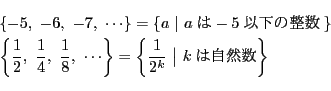
整数の部分集合でも，そのうち正の要素からなる部分集合には最小の要素が存在する． 一次不定方程式の解の存在の証明に，この最小要素の存在を用いるところがある．

(iii) 数学的帰納法の原理

$\mathbb{N}$の部分集合 $A$ が条件：

$$1 \in A ，かつ\ x\in A\ なら\ x+1 \in A$$

を満たすなら，$A$ は $\mathbb{N}$ 自身である．

これがなぜ数学的帰納法の原理なのか．

すべての自然数$n$であることが成り立つことを示すときに用いる数学的帰納法という証明方法がある． $n=1$のときに成り立ち，$n=k$のときに成り立つと仮定すると$n=k+1$でも成り立つ． するとこれですべての自然数で成り立つと言える．有理数や実数ではこうはいかない． ということは，この証明方法が可能な根拠は自然数の性質にあるということになる．

それが(iii) 数学的帰納法の原理である． これはどういうことを言っているのか． このことの理解は高校範囲を越えるのであるが， 自然数の大切な性質なので書いておこう．

$p(n)$ を自然数 $n$を含む命題とする． 数学的帰納法とは， すべての自然数$n$で$p(n)$が真であることを証明するための， 次のような証明方法であった．

(1)

$p(1)$が真である．

(2)

$p(k)$が真なら$p(k+1)$が真である．

(3)

(1), (2)より, すべての自然数 $n$ に対して $p(n)$が真である．

この証明方法ですべての自然数で成立することが， (iii) 数学的帰納法の原理から次のように示される．

条件$p(n)$が成立する自然数$n$よりなる$\mathbb{N}$の部分集合を$A$とする． つまり

$$A=\{n\ \vert\ n \in \mathbb{N},\ かつ\ p(n)が成立する．\}$$

とおく．数学的帰納法の(1)は$1\in A$，(2)は$k\in A$なら$k+1\in A$が成り立つことを示している． すると自然数の性質(iii)より$A=\mathbb{N}$． つまりすべての自然数 $n$ に対して $p(n)$が成立する．

(証明終わり)

このように数学的帰納法は，自然数の性質を根拠とする証明法である．

自然数の演算

自然数の集合$\mathbb{N}$の要素$a$と$b$の和$a+b$，積$ab$は再び$\mathbb{N}$に属する． また和と積に関して

$$a(x+y)=ax+ay$$

が成り立つ．この公式を分配法則という． また，演算の結果がふたたびその集合に属することをその演算に関して閉じているという． 自然数の集合は$\mathbb{N}$は加法と乗法に関して閉じている． これに対して減法と除法については閉じていない．

$\mathbb{N}$を含み加法・減法で閉じている最小の集合が整数の集合$\mathbb{Z}$であり， $\mathbb{Z}$を含み乗法・除法で閉じている最小の集合が有理数の集合$\mathbb{Q}$である．