まず整式に関する用語の確認をする.
- 整式
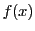 が整式
が整式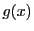 の約数であるとは
の約数であるとは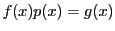 を満たす整式
を満たす整式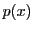 が存在することをいう.
が存在することをいう.
- 整式
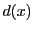 が2つの整式
が2つの整式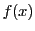 ,
,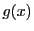 の公約数であるとは,
の公約数であるとは,
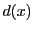 が
が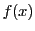 の約数であり,かつ,
の約数であり,かつ,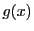 の約数でもあることをいう.
の約数でもあることをいう.
- 整式
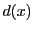 が2つの整式
が2つの整式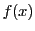 ,
,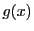 の最大公約数であるとは,
の最大公約数であるとは,
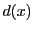 が
が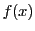 ,
,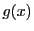 の公約数の中で次数が最大のものであることをいう.
(
の公約数の中で次数が最大のものであることをいう.
(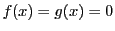 の場合は除く).
の場合は除く).
- (1)
- 整式
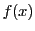 は
は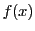 の約数であることを示せ.
の約数であることを示せ.
- (2)
- 0と異なる整式
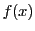 が整式
が整式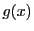 の約数であれば,
の約数であれば,
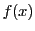 は
は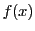 ,
,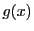 の最大公約数であることを示せ.
の最大公約数であることを示せ.
- (3)
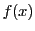 が0とは異なる整式で,
整式
が0とは異なる整式で,
整式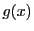 を
を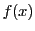 で割った余りが
で割った余りが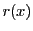 であるとする.
いま,整式
であるとする.
いま,整式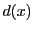 が
が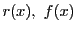 の最大公約数であるとすれば,
の最大公約数であるとすれば,
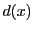 は
は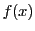 ,
,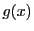 の最大公約数でもあることを示せ.
の最大公約数でもあることを示せ.