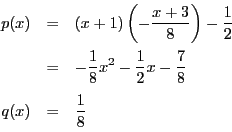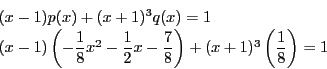- (1)
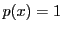 とすれば
とすれば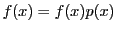 となるので,
整式
となるので,
整式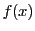 は
は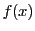 の約数である.
の約数である.
- (2)
- 0と異なる整式
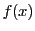 が整式
が整式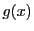 なので,(1)から
なので,(1)から
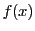 は
は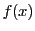 ,
,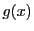 の公約数である.
の公約数である.
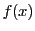 の約数の次数は
の約数の次数は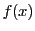 の次数以下であるから,
の次数以下であるから,
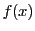 は
は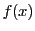 と
と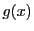 の公約数のなかで次数最大である.
つまり
の公約数のなかで次数最大である.
つまり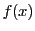 は
は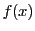 ,
,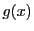 の最大公約数である.
の最大公約数である.
- (3)
- 整式
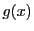 を
を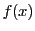 で割った商を
で割った商を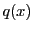 とすると,
とすると,
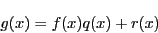
である.整式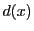 が
が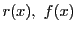 の公約数なので,
の公約数なので,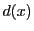 は
は
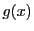 の約数ともなり,
の約数ともなり,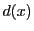 は
は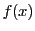 ,
,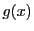 の公約数でもある.
の公約数でもある.
ここで
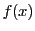 ,
,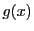 の最大公約数を
の最大公約数を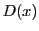 とすると,
とすると,
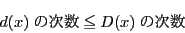
つぎに
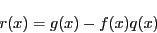
より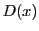 は
は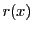 の約数にもなり,
の約数にもなり,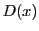 は
は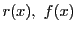 の公約数となる.
この結果
の公約数となる.
この結果
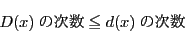
あわせて
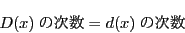
となり,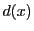 が
が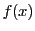 ,
,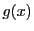 の最大公約数でもあることが示された.
の最大公約数でもあることが示された.
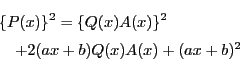
![\begin{eqnarray*}
&&Q(x)\left[B(x)-Q(x)\{A(x)\}^2\right.\\
&&\quad\left.-2(ax+b)A(x)\right]=(ax+b)^2
\end{eqnarray*}](images/img1002.gif)
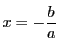 を持つ.
を持つ.
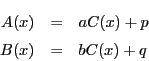
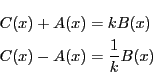
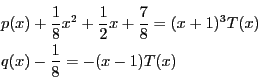
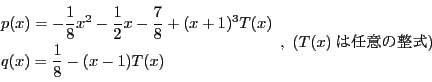
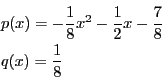
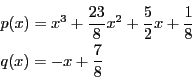
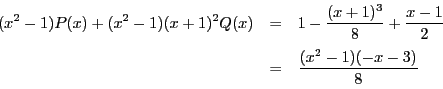
 .
.