次: 演習問題 上: 整数の約数と倍数 前: 約数・倍数と最大公約数

ユークリッドの互除法

24と42の最大公約数を求めようとすれば，いずれをも割り切る素数を見い出して， 順に割っていくのだ．

$$\begin{array}{rcc} 2)&24&42\\ \hline 3)&12&21\\ \hline &4&7 \end{array} \quad \quad ∴\quad (24,\ 42)=6$$

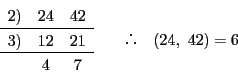
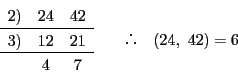
しかしこの方法には欠点がある．暗算で見つかるような小さい素数なら順次調べればよいが， 6188と4709 のなかの素数のように少し大きいと，発見するのはなかなか難しい．

ところが，つねに最大公約数を見い出すことのできる方法がある！　 それがユークリッドの互除法である．その根拠は次のような除法の式からの結論である．

定理 3        $a>b>0$を整数とし, $a$を$b$で割った余りを$r$とすると， $(a,\ b)=(r,\ b)$である．

証明     $a$を$b$で割った商を$q$とする．$a=bq+r$である．

$(a,\,b)=d_1$ とすると $a=a'd_1,\;b=b'd_1$ とおける.

$$r=a'd_1-b'd_1q=d_1(a'-b'q)$$

これより$r$ も $d_1$ で割れる. よって,$d_1$ は $b$と$r$ の公約数となり， $d_1\le (b,\,r)=d_2$．

次に$(b,\,r)=d_2$ とすると, $b=b'd_2,\;r=r'd_2$ とおける.

$$a= b'd_2q+r'd_2= d_2(b'q+r')$$

より同様に $d_2\le (a,\,b)=d_1$．よって $d_1=d_2$ ，つまり $(a,\,b)=(b,\,r)$である． (証明終わり)

ここで除法の定理により $0 \le r<b$ である．余りはもとの数より小さい． 最大公約数をより小さい数の間の最大公約数を求める問題に還元してゆくことができるのではないか． つまり，割り算をくりかえして最大公約数を追いつめることができる．これは大きな発見だった．

実際にやってみよう．

例 1        $(6188,4709)$を求めよう． 順次割り算を行う．

$$\begin{eqnarray*} &&6188=4709\times 1+1479\\ &&4709=1479\times 3+272\\ &... ...72=119\times 2+34\\ &&119=34\times3+17\\ &&34=17\times 2 \end{eqnarray*}$$

これより最大公約数の次の系列を得る．

$$\begin{eqnarray*} &&(6188,\,4709)=(4709,\,1479)=(1479,\,272)\\ &=&(272,\,119)=(119,\,34)=(34,\,17)=17 \end{eqnarray*}$$

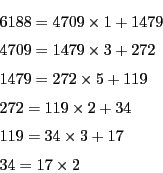
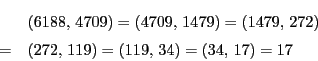
こうして確かに最大公約数が求まる．この方法をユークリッドの互除法という．

「必ずできる一般的方法」をアルゴリズムという．ユークリッドの互除法はアルゴリズムの基本例である． その他の有名なアルゴリズムは2次方程式の解法である．平方完成して移項して平行根をとることにより解ける． この過程を一つにまとめたのが2次方程式の解の公式である．

ユークリッド

「ユークリッド」は英語圏での書き方(英語表記 Euclid)とその読み方で，本来は「エウクレイデス」と発音する．

エウクレイデス（Eukleides，紀元前365年?〜紀元前275年?）は古代ギリシアの数学者，天文学者とされる人で，アテナイで学びプトレマイオス1世治下のアレクサンドリアで教えた．ちなみにプトレマイオス1世とは，アレクサンドロス3世（アレキサンダー大王）の部下であったマケドニア地方出身のギリシア人で，大王の死後，エジプトの支配を継ぎ，プトレマイオス朝を創始した．

『原論』はラテン語圏，アラビア語圏にもたらされ，その後各地で二千数百年にわたって幾何学，いや数学そのもの基本となる書物であった．この書は13巻から成り，1〜6巻は平面幾何，7〜9巻は数論，10巻は無理量，11〜13巻は立体幾何を取り扱っている． 最大公約数を求める方法であるユークリッドの互除法はこの『原論』にある．