
 次: ラムゼー数
上: ラムゼー型定理
次: ラムゼー数
上: ラムゼー型定理
太郎
次のような問題に出会いました.鳩の巣原理を使う練習問題でした.
例題 0.1
- 6人の人がいる.
どの2人も,互いに知り合いであるかまたは見ず知らずであるか,いずれかとする.
すると,お互いに知り合いである3人がいるか,
お互いに見ず知らずである3人がいるか,いずれかが成り立っていることを示せ.
- 平面に17個の点がある.各2点は赤,青,黒のいずれかの線分で結ばれている.
このとき3辺が同じ色の三角形が存在することを示せ.
解答
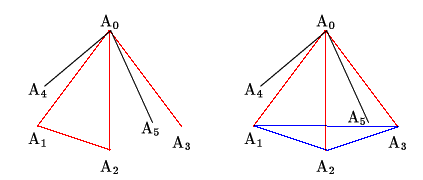
- 6人を平面上の6点
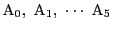 に対応させる.
知り合いの場合は赤の線分で結び,
見ず知らずの場合は青の線分で結ぶ.
に対応させる.
知り合いの場合は赤の線分で結び,
見ず知らずの場合は青の線分で結ぶ.
点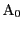 からは5本の線分が出ている.
からは5本の線分が出ている.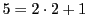 なので赤か青かのいずれかは
3本以上である.赤が3本以上出ているとし,
なので赤か青かのいずれかは
3本以上である.赤が3本以上出ているとし,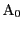 とそれらの線分で結ばれた点のうち
の3点を
とそれらの線分で結ばれた点のうち
の3点を
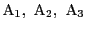 とする.
この3点を結ぶ3本の線分のなかに赤があるとする.
それを
とする.
この3点を結ぶ3本の線分のなかに赤があるとする.
それを
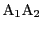 とすると,
3点
とすると,
3点
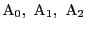 に対応する3人は互いに知り合いである.
に対応する3人は互いに知り合いである.
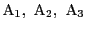 を結ぶ3本の線分がすべて青とする.この場合,
この3点に対応する3人は互いに見ず知らずである.
を結ぶ3本の線分がすべて青とする.この場合,
この3点に対応する3人は互いに見ず知らずである.
赤青逆の場合も同様に示される.
- 17個の点を
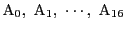 で表す.これらの点が互いに青色,赤色,黒色の線分で結ばれている.
で表す.これらの点が互いに青色,赤色,黒色の線分で結ばれている.
点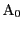 から出ている16本の線分を考える.
から出ている16本の線分を考える.
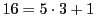 なので,少なくともひとつの色については6本の線分が出ている.その色を
青とし,それらの端点を
なので,少なくともひとつの色については6本の線分が出ている.その色を
青とし,それらの端点を
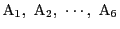 とする.
とする.
これら6個の点を結ぶ線分の中に青色があればその線分の両端の点と
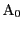 でできる三角形が題意を満たす.
でできる三角形が題意を満たす.
もしこれらの線分が赤色と黒色のみであったとする.
この6点のうちには(1)により,赤か黒の三角形が少なくとも一つは存在する.
したがって3辺が同じ色の三角形が存在することが示された.
太郎 これを 有限個の点がある.各2点を定まった色で塗り分ける場合, 点がいくつあれば,3辺が同色の三角形がつねに存在すると言えるのか.
という問題に一般化してみました.
色の数を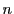 とし,次の漸化式で定まる数列
とし,次の漸化式で定まる数列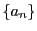 を考えました.
色が一色の場合,3点あればよいので,
を考えました.
色が一色の場合,3点あればよいので,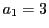 とします.
とします.
定理 1
次の漸化式で数列
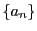
を定める.
平面上に
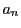
個の点がある.
各2点をどのように
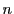
色で塗り分けても,
つねに同色の三角形が存在する.
■
証明
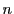 に関する数学的帰納法で示す.
に関する数学的帰納法で示す.
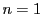 のときは成立するので,
のときは成立するので,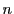 のとき
のとき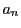 点あれば同色の3辺の三角形が存在するとする.
点あれば同色の3辺の三角形が存在するとする.
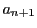 個の点を
個の点を
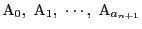 で表す.これらの点が互いに色1,色2,…色
で表す.これらの点が互いに色1,色2,…色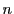 の線分で結ばれている.
の線分で結ばれている.
点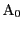 から出ている
から出ている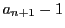 本の線分を考える.
本の線分を考える.
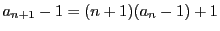 なので,少なくともひとつの色については
なので,少なくともひとつの色については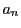 本の線分が出ている.
その色を色1とし,それらの端点を
本の線分が出ている.
その色を色1とし,それらの端点を
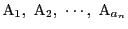 とする.
とする.
これら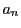 個の点を結ぶ線分の中に色1があればその線分の両端の点と
個の点を結ぶ線分の中に色1があればその線分の両端の点と
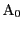 でできる三角形が題意を満たす.
でできる三角形が題意を満たす.
もしこれらの線分が色2〜色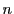 であったとする.
この
であったとする.
この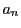 点のうちには帰納法の仮定によって,3辺が色2〜色
点のうちには帰納法の仮定によって,3辺が色2〜色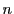 のいずれかの三角形が少なくとも一つは存在する.
のいずれかの三角形が少なくとも一つは存在する.
したがって3辺が同じ色の三角形が存在することが示された.
□
太郎
この一般項は求まるのでしょうか.
南海
このように問題を一般化してとらえようとすることは,大切なことだ.
次のようにすれば,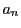 を書くことができる.
を書くことができる.
と変形する.よって
である.一方,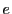 を自然対数の底とすると
を自然対数の底とすると
であるが,ここで
よって
つまり
この結果
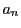 は正整数なので,
は正整数なので,
と表される.ただし,実数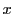 に対して
に対して![$[x]$](images/img31.gif) は
は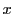 を超えない最大の整数を表す.
□
を超えない最大の整数を表す.
□
太郎
確かに
です.
太郎
色の数を一般化しましたが,さらに一般化はできるのでしょうか.
南海
2点ずつ結んだ線分を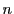 色で塗り分ける.
色で塗り分ける.
3点を選ぶとその3つの辺の色が同じである.
を
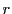 個の点を結んだ多辺形を
個の点を結んだ多辺形を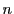 色で塗り分ける.
色で塗り分ける.
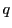 個の点を選ぶとそのうちの
個の点を選ぶとそのうちの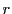 個の点を結んだ多辺形はいずれも色が同じである.
個の点を結んだ多辺形はいずれも色が同じである.
とする.また集合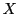 の各元を
の各元を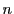 色で塗り分けるとは,
色で塗り分けるとは,
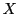 から,
から,
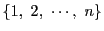 への写像を定めることに他ならない.
さらに「
への写像を定めることに他ならない.
さらに「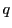 個の点」と言うところを,色によってその個数の指定を変えてもよい.
つまり
個の点」と言うところを,色によってその個数の指定を変えてもよい.
つまり
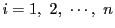 に対して「
に対して「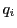 個の点」としたほうがより一般的になる.
個の点」としたほうがより一般的になる.
その上で,先の問題を一般化すれば次のようになる.
集合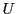 の
の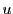 個の元からなるすべての部分集合の集合を
個の元からなるすべての部分集合の集合を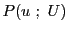 と表す.
と表す.
今後は,色の塗り分けで考えたり,写像 で考えたりするが,
それは同じことである.
で考えたりするが,
それは同じことである.

 次: ラムゼー数
上: ラムゼー型定理
Aozora
次: ラムゼー数
上: ラムゼー型定理
Aozora
2015-03-04
![]() からは5本の線分が出ている.
からは5本の線分が出ている.![]() なので赤か青かのいずれかは
3本以上である.赤が3本以上出ているとし,
なので赤か青かのいずれかは
3本以上である.赤が3本以上出ているとし,![]() とそれらの線分で結ばれた点のうち
の3点を
とそれらの線分で結ばれた点のうち
の3点を
![]() とする.
この3点を結ぶ3本の線分のなかに赤があるとする.
それを
とする.
この3点を結ぶ3本の線分のなかに赤があるとする.
それを
![]() とすると,
3点
とすると,
3点
![]() に対応する3人は互いに知り合いである.
に対応する3人は互いに知り合いである.
![]() を結ぶ3本の線分がすべて青とする.この場合,
この3点に対応する3人は互いに見ず知らずである.
を結ぶ3本の線分がすべて青とする.この場合,
この3点に対応する3人は互いに見ず知らずである.
![]() から出ている16本の線分を考える.
から出ている16本の線分を考える.
![]() なので,少なくともひとつの色については6本の線分が出ている.その色を
青とし,それらの端点を
なので,少なくともひとつの色については6本の線分が出ている.その色を
青とし,それらの端点を
![]() とする.
とする.
![]() でできる三角形が題意を満たす.
でできる三角形が題意を満たす.
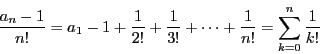
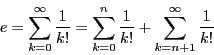
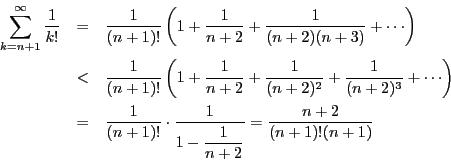
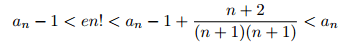
![\begin{displaymath}
\begin{array}{l}
a_1=[e+1]=3,\ a_2=[2e+1]=6,\ \\
a_3=...
...7\ (17.2=6\cdot 2.7+1<6e+1<6\cdot 2.72+1=17.32)
\end{array}
\end{displaymath}](images/img32.gif)