南海
![]() ならその中に一定の構造が存在する,これが成り立つ
ならその中に一定の構造が存在する,これが成り立つ![]() の存在は示せた.
次の問題は
の存在は示せた.
次の問題は![]() の上限と下限を求めるということだ.
しかし一般にこれはたいへん難しい.
とくに下限はほとんどの場合わからない.
の上限と下限を求めるということだ.
しかし一般にこれはたいへん難しい.
とくに下限はほとんどの場合わからない.
太郎
そうなのですね.色の数を![]() にした場合,三角形ができるための上限公式は先に導けました.
にした場合,三角形ができるための上限公式は先に導けました.
南海
ここで,![]() つまり2点を結ぶ線分を
つまり2点を結ぶ線分を![]() 色で塗り分ける場合に一般化しよう.
色で塗り分ける場合に一般化しよう.
![]() のときは
のときは
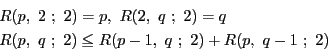
太郎
![]() は何を意味していたか再確認します.
は何を意味していたか再確認します.
自然数
![]() をとる.
をとる.![]() 個の点の集合を
個の点の集合を![]() とする.
とする.
![]() の2点を結ぶ線分を赤色と青色で塗り分ける.
の2点を結ぶ線分を赤色と青色で塗り分ける.
![]() の
の![]() 個からなる部分集合
個からなる部分集合![]() でその線分がすべて赤色か,
でその線分がすべて赤色か,
![]() 個からなる部分集合
個からなる部分集合![]() でその線分がすべて青色であるものが存在する.
でその線分がすべて青色であるものが存在する.
![]() を示します.
を示します.
![]() 個以上の点の集合を
個以上の点の集合を![]() とする.
とする.
![]() の2点を結ぶ線分を赤色と青色で塗り分ける.
すべてが赤色で塗られていれば
の2点を結ぶ線分を赤色と青色で塗り分ける.
すべてが赤色で塗られていれば![]() とする.
青色の線分が存在すれば,その2点を
とする.
青色の線分が存在すれば,その2点を![]() とする.
とする.
この部分はこれでいいでしょうか.
南海
いや,![]() 以下ではできない反例を示すことが必要だ.
以下ではできない反例を示すことが必要だ.
太郎
![]() 以下の場合,すべてを赤でぬれば,
以下の場合,すべてを赤でぬれば,
![]() の
の![]() 個からなる部分集合
個からなる部分集合![]() でその線分がすべて赤色のものも,
でその線分がすべて赤色のものも,
![]() 個からなる部分集合
個からなる部分集合![]() でその線分がすべて青色であるものも存在しません.
でその線分がすべて青色であるものも存在しません.
南海 そう.これ自体は難しくないが,このように下の限界を示すことが大切なのだ.
太郎
つぎに不等式を示すためには,
![]() であれば,
先の命題が成り立つことを示せばよい.
であれば,
先の命題が成り立つことを示せばよい.
不等式
右辺は,![]() 個の集合の各2点を結ぶ線分を2色で着色すれば,
赤の線分が
個の集合の各2点を結ぶ線分を2色で着色すれば,
赤の線分が
![]() あるか,
青の線分が
あるか,
青の線分が
![]() あるかを意味します.
あるかを意味します.
いずれもがなければ,その合計は
![]() より小さいはずだからです.
より小さいはずだからです.
![]() 個の点の一つを固定し,そこから残る
個の点の一つを固定し,そこから残る![]() 個の点を赤か青の線分で結ぶ.
このとき,赤の線分の端点が
個の点を赤か青の線分で結ぶ.
このとき,赤の線分の端点が
![]() 以上あるか,
青の線分の端点が
以上あるか,
青の線分の端点が
![]() 以上あるか,その少なくとも一方は成り立つ.
以上あるか,その少なくとも一方は成り立つ.
赤の線分の端点が
![]() 以上あるとする.
それらの端点の
以上あるとする.
それらの端点の![]() 個からなる部分集合
個からなる部分集合![]() でその線分がすべて青色であるものが存在するなら,それでよい.
それらの端点の
でその線分がすべて青色であるものが存在するなら,それでよい.
それらの端点の![]() 個からなる部分集合
個からなる部分集合![]() でその線分がすべて赤色であるものが存在するなら,
それにはじめの1点を加えた
でその線分がすべて赤色であるものが存在するなら,
それにはじめの1点を加えた![]() 個からなる部分集合
個からなる部分集合![]() はその線分がすべて赤色である.
はその線分がすべて赤色である.
青の線分の端点が
![]() 以上ある場合も同様である.
以上ある場合も同様である.
したがって,![]() が
が
![]() 以上であることは,
以上であることは,
![]() の
の![]() 個からなる部分集合
個からなる部分集合![]() でその線分がすべて赤色か,
でその線分がすべて赤色か,
![]() 個からなる部分集合
個からなる部分集合![]() でその線分がすべて青色であるものが存在するための十分条件である.
でその線分がすべて青色であるものが存在するための十分条件である.
よってその最小値
![]() は
は
太郎
この考え方なら色の数![]() がの場合も同じことですね.
ここで書いてみます.
がの場合も同じことですね.
ここで書いてみます.
定理4の証明
![]() のとき.
のとき.
![]() を示す.
を示す.
![]() 個以上の点の集合を
個以上の点の集合を![]() とする.
とする.
![]() の2点を結ぶ線分を
の2点を結ぶ線分を![]() 色で塗り分ける.
すべてが
色で塗り分ける.
すべてが![]() 色で塗られていれば
色で塗られていれば![]() とする.
とする.
![]() 色以外の線分が存在すれば,その色を
色以外の線分が存在すれば,その色を![]() とするとき,その2点を
とするとき,その2点を![]() とする.
とする.
![]() 以下の場合,すべてを
以下の場合,すべてを![]() 色でぬれば,
色でぬれば,
![]() の
の![]() 個からなる部分集合
個からなる部分集合![]() でその線分がすべて
でその線分がすべて![]() 色のものも,
色のものも,
![]() 個からなる部分集合
個からなる部分集合![]() でその線分がすべて
でその線分がすべて![]() 色であるものも存在しない.
色であるものも存在しない.
次に不等式は
![]() をとり,
をとり,![]() 個の点の一つを固定する.
そこから残る
個の点の一つを固定する.
そこから残る![]() 個の点を
個の点を![]() 色で塗り分ける.
このとき,
色で塗り分ける.
このとき,
![]() なので,
なので,
![]() 色の線分の端点が
色の線分の端点が
![]() 以上あるような
以上あるような![]() が存在する.
が存在する.
![]() に対し端点の
に対し端点の![]() 個からなる部分集合
個からなる部分集合![]() でその線分がすべて
でその線分がすべて![]() 色であるものが存在するなら,それでよい.
それらの端点の
色であるものが存在するなら,それでよい.
それらの端点の![]() 個からなる部分集合
個からなる部分集合![]() でその線分がすべて
でその線分がすべて![]() 色であるものが存在するなら,
それにはじめの1点を加えた
色であるものが存在するなら,
それにはじめの1点を加えた![]() 個からなる部分集合
個からなる部分集合![]() はその線分がすべて
はその線分がすべて![]() 色である.
したがって,この
色である.
したがって,この![]() に対して
に対して![]() の
の![]() 個からなる部分集合
個からなる部分集合![]() でその線分がすべて
でその線分がすべて![]() 色であるものが存在した.
□
色であるものが存在した.
□
太郎 上限に関する漸化不等式ができたので,これから具体的に上限を表したいです.
南海
定理4は![]() のときはきれいな形である.この場合は可能だ.
のときはきれいな形である.この場合は可能だ.
太郎
![]() のときは
のときは
![]() でした.
でした.
一般の場合は難しそうです.
南海 さらに下限を確定することは難しい.