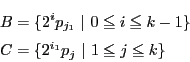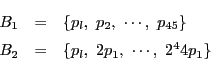次: 参考書
上: ラムゼー型定理
前: 漸化不等式
太郎
下限の確定が難しいということですが,2014年の次の問題では,上限と下限が一致しました.
次のは青空学園の解答です.
次: 参考書
上: ラムゼー型定理
前: 漸化不等式
太郎
下限の確定が難しいということですが,2014年の次の問題では,上限と下限が一致しました.
次のは青空学園の解答です.
解答
- 奇数の素数は無限個ある.相異なる奇数の素数を
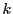 個選びそれを
個選びそれを
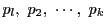 とする.このとき
とする.このとき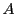 を
を
で定める.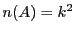 である.
である.
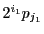 と
と
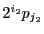 は,
は,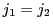 なら一方が他方を割り切り,
なら一方が他方を割り切り,
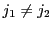 なら互いに他方を割り切らない.
なら互いに他方を割り切らない.
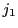 や
や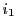 を固定し
を固定し
とおく.それぞれ要素の個数は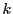 である.
である.
このとき,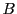 は良い集合である.
また
は良い集合である.
また 個以上の要素からなる部分集合には,
素数部分が相異なる2数が含まれる.
その2数は互いに他方を割り切らない.
よつて
個以上の要素からなる部分集合には,
素数部分が相異なる2数が含まれる.
その2数は互いに他方を割り切らない.
よつて 個以上の要素からなる良い部分集合は存在しない.
個以上の要素からなる良い部分集合は存在しない.
このとき,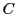 は悪い集合である.
また
は悪い集合である.
また 個以上の要素からなる部分集合には,素数部分が等しい2数が含まれる.
その2数は一方が他方を割り切る.
よって
個以上の要素からなる部分集合には,素数部分が等しい2数が含まれる.
その2数は一方が他方を割り切る.
よって 個以上の要素からなる悪い部分集合は存在しない.
個以上の要素からなる悪い部分集合は存在しない.
これから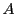 は最良数も最悪数も
は最良数も最悪数も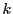 となる集合である.
となる集合である.
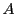 の要素
の要素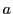 に対し,
に対し,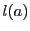 を,
を,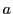 を最小の要素として含む良い集合のなかで,
要素の個数が最大のもののその個数とする.つまり
を最小の要素として含む良い集合のなかで,
要素の個数が最大のもののその個数とする.つまり
そして
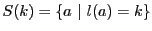 とおく.
とおく.
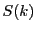 は悪い集合である.
なぜなら,もし
は悪い集合である.
なぜなら,もし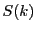 の2要素
の2要素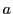 と
と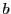 で
で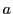 が
が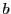 を割るものがあれば
を割るものがあれば
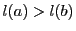 となるからである.
となるからである.
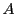 の部分集合
の部分集合
を考える.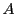 の要素でこの部分集合に入らないものがあれば,
それを最小の要素として含む良い集合は
の要素でこの部分集合に入らないものがあれば,
それを最小の要素として含む良い集合は 以上の要素からなり,
最良数は
以上の要素からなり,
最良数は 以上である.
以上である.
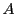 のすべての要素がこのうちのいずれかに入れば,
のすべての要素がこのうちのいずれかに入れば,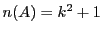 なので,
どれかは
なので,
どれかは 以上の要素からなる.
つまり
以上の要素からなる.
つまり 個以上からなる悪い集合が存在し,最悪数が
個以上からなる悪い集合が存在し,最悪数が 以上となる.
以上となる.
-
である.
最良数と最悪数が等しいとき,その個数を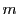 と置くと,(2)の議論から
と置くと,(2)の議論から
この結果
が必要である.
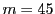 で
で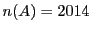 となるものを構成すれば,それが例になる.
となるものを構成すれば,それが例になる.
(1)で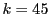 として構成した集合を
として構成した集合を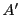 とする.
とする.
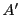 の部分集合
の部分集合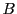 を
を
とする.これは89個の要素からなる.この部分集合
がそれぞれ最悪数と最良数45を与える.
集合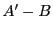 から任意に,要素の個数が
から任意に,要素の個数が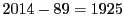 の部分集合
の部分集合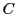 を選ぶ.
を選ぶ.
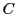 の良い集合や悪い集合の要素の個数は45を超えず,
また
の良い集合や悪い集合の要素の個数は45を超えず,
また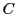 のどの要素を
のどの要素を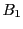 や
や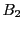 に加えても,それぞれ最悪数や最良数を増やすことはない.
に加えても,それぞれ最悪数や最良数を増やすことはない.
よって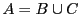 とすると,
とすると,
である集合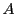 が構成された. □
が構成された. □
(2)の別解
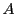 のすべての要素を次の原則を満たすように,上下に並ぶ平行な直線上に配置する.
のすべての要素を次の原則を満たすように,上下に並ぶ平行な直線上に配置する.
- (i)
- 倍数を上段に置き,割る数と割られる数を結ぶ.
- (ii)
- 割る数と割られる数が隣りあう平行線上に置けるときは置く.
- (iii)
- 結びあう数がないものは最下段に置く.
たとえば本問の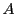 は次のようになる.
は次のようになる.
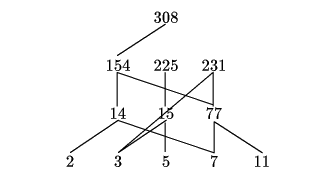
原則(ii)によって,最下段から最上段の数まで一段ずつ数のある折れ線が存在する.
よって段数が最良数である.
また同じ段にある数は,互いに他方を割り切らず,その集合は悪い部分集合である.
その要素の個数は最悪数を超えない.
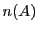 は各段の要素の個数を加えたものであるから
は各段の要素の個数を加えたものであるから
である.
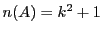 のとき,
のとき,
と仮定すると,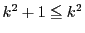 となり,矛盾する.
となり,矛盾する.
よって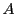 の最悪数と最良数の少なくとも一方は
の最悪数と最良数の少なくとも一方は 以上である.
□
以上である.
□
太郎
そういえば,上限が同様な数となる例題を見たことがあります.
例題 0.3
1から
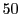
までのカードが1枚ずつある.
これらのカードを1列に並べ,それを
とする.ここから
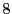
枚のカードを抜き出し順序を変えずに
とする.このとき
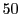
枚のカードをどのように並べても,かならず
となるものが選び出せることを示せ.
解答
並べられた50枚のカード
の各々に次のように数の組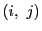 を対応させる.
を対応させる.
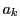 からはじまって右方に伸びる増加列の最大長を
からはじまって右方に伸びる増加列の最大長を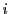 ,
減少列の最大長を
,
減少列の最大長を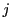 とする.このときカード
とする.このときカード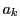 に
に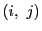 を対応させる.
を対応させる.
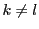 のとき,
のとき,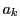 に対応する
に対応する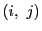 と,
と,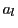 に対応する
に対応する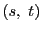 は異なる.
なぜなら,
は異なる.
なぜなら,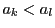 なら
なら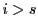 であるし,
であるし,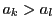 なら
なら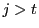 であるからである.
であるからである.
そこで,
このとき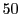 枚のカードのどのような並べ方に対しても,
枚のカードのどのような並べ方に対しても,
となるものが選び出せなかったとする.
この場合,最大長が7以下なので50枚のカードに対応させた数の組
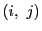 に現れる
に現れる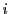 も
も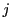 もすべて7以下であるということを意味する.
もすべて7以下であるということを意味する.
ところがこのような数の組は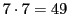 組しかない.
したがって50枚のカードに対応させた数の組には少なくとも1組同じものがなければならない.
組しかない.
したがって50枚のカードに対応させた数の組には少なくとも1組同じものがなければならない.
これは
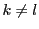 のとき,
のとき,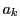 に対応する
に対応する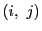 と,
と,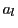 に対応する
に対応する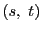 は異なる,
という結果と矛盾する.
は異なる,
という結果と矛盾する.
したがって背理法によって題意が示された.
□
太郎
この50と8の関係が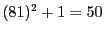 で
8の代わりに
で
8の代わりに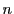 にして,50を
にして,50を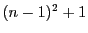 にしても,まったく同様に示せます.
にしても,まったく同様に示せます.
2014年の早稲田の問題を参考に知ると,次の別解ができました.
一般の場合でやってみます.
別解
カード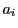 に対し,
に対し,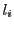 を,
を,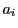 から始まる増加列で最長のものの長さとする.
そして
から始まる増加列で最長のものの長さとする.
そして
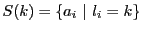 とおく.
とおく.
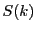 は減少列である.
なぜなら,もし
は減少列である.
なぜなら,もし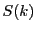 の2要素
の2要素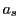 と
と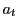 で
で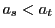 となるものがあれば
となるものがあれば
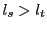 となるからである.
となるからである.
集合
を考える.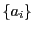 でこの集合に入らないものがあれば,
それから始まる増加列は
でこの集合に入らないものがあれば,
それから始まる増加列は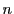 以上である.
以上である.
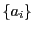 がすべてこの集合に入れば,
がすべてこの集合に入れば,
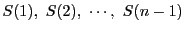 のどれかは
のどれかは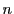 以上の要素からなる.
もしすべて
以上の要素からなる.
もしすべて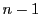 以下なら総数が高々
以下なら総数が高々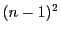 だからである.
よって総数が
だからである.
よって総数が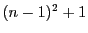 なら,
なら,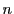 個以上からなる減少列が存在する.
□
個以上からなる減少列が存在する.
□
南海
これはよく考えている.
太郎
この2つは同じ問題でしょうか.
南海
まず,例題0.3はErdös-Szekeres(エルディシュ-ゼッカーズ)の定理といわれる美しい定理である.
この語で検索してみると,さまざまの証明法などもある.
また,これは離散幾何といわれる分野に関わる.
これについてもここでは宿題にしておこう.
その上で,例題0.3と例題0.3は異なる.
例題0.3では,集合の中に2つの関係が入っている.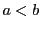 か
か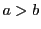 である.そして一方の否定が他方になる.
この2つの関係は,いずれも順序の関係を満たす.
である.そして一方の否定が他方になる.
この2つの関係は,いずれも順序の関係を満たす.
が成り立つ.
太郎
そうか.例題0.3では,「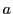 は
は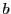 の倍数である」という関係は順序の関係を満たすが
その否定「
の倍数である」という関係は順序の関係を満たすが
その否定「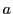 は
は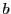 の倍数でない」は順序の関係は満たさない.
だから例題0.3を,数の組
の倍数でない」は順序の関係は満たさない.
だから例題0.3を,数の組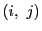 を考えることで示すことはできないのです.
を考えることで示すことはできないのです.
南海
そういうことだ.さらに,一般の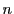 についてErdös-Szekeresの定理でいう増加列や減少列が存在するための必要条件は確定していないはずだ.最近の結果までは確認できないが,たいへん難しい問題であることまちがいない.
についてErdös-Szekeresの定理でいう増加列や減少列が存在するための必要条件は確定していないはずだ.最近の結果までは確認できないが,たいへん難しい問題であることまちがいない.
太郎
例題0.3は,論理的に導いた上限が下限でもあるという,その意味ではまれな場合なのですね.
南海
こういう離散数学は,日本の高校ではあまり重視されない分野であるのだが,
2014年の入試問題もあり,その背後に広がる分野について対話できたことは,意味があった.


 次: 参考書
上: ラムゼー型定理
前: 漸化不等式
Aozora
次: 参考書
上: ラムゼー型定理
前: 漸化不等式
Aozora
2015-03-04
![]() とする.
とする.
![]() のどの2数も一方が他方を割り切るとき
のどの2数も一方が他方を割り切るとき![]() は良い集合であるといい,
は良い集合であるといい,![]() のどの2数も互いに他を割り切らないとき
のどの2数も互いに他を割り切らないとき![]() は悪い集合であるという.
は悪い集合であるという.
![]() の良い部分集合の要素の個数の最大値,すなわち,
の良い部分集合の要素の個数の最大値,すなわち,
![]() のとき,
のとき,
![]() の良い部分集合は
の良い部分集合は
![]() ,
,
![]() ,
,
![]() などであり,
などであり,![]() の最良数は4である.
また,
の最良数は4である.
また,![]() の悪い部分集合は
の悪い部分集合は
![]() ,
,
![]() ,
,
![]() ,
,
![]() などであり,
などであり,![]() の最悪数は5である.
の最悪数は5である.
![]() を2以上の整数とするとき,次の問いに答えよ.
を2以上の整数とするとき,次の問いに答えよ.
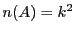 で,かつ最良数も最悪数も
で,かつ最良数も最悪数も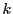 である集合
である集合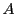 が存在することを証明せよ.
が存在することを証明せよ.
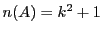 ならば,
ならば,
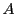 の最良数または
の最良数または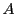 の最悪数のどちらかは
の最悪数のどちらかは 以上であることを証明せよ.
以上であることを証明せよ.
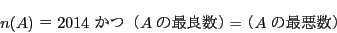
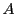 を考える.このような集合たちの中で最良数が最小となる集合の例を挙げよ.
を考える.このような集合たちの中で最良数が最小となる集合の例を挙げよ.