距離という以上,それは負でない実数値が定まり,
また点![]() と点
と点![]() の距離が
点
の距離が
点![]() と点
と点![]() の距離に等しく,
さらに
の距離に等しく,
さらに![]() であることは
であることは
![]() と同値でなければならないだろう.
と同値でなければならないだろう.
しかしこれだけで距離とすると,実はいろいろな距離ができすぎる. つまり余りに広い定義は,数学の定義としては意味がないのだ. もう少し,これこそ距離だ,といえるように距離を特徴づけなければならない.
そのために,われわれの日頃使っている距離について調べておかねばならない.
2点
![]() と
原点
と
原点![]() に対して,
に対して,
![]() が成立しているとする.
つまりどの3点も同一直線上にないとする.
が成立しているとする.
つまりどの3点も同一直線上にないとする.
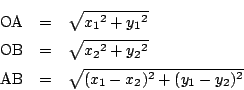
美樹 これらの間の関係って,三角形の成立条件ですか.
南海 そうだ.そこでまず三角形の成立条件とは何か.
美樹
3つの正数![]() を3辺の長さとする三角形が存在するための
必要十分条件は,不等式
を3辺の長さとする三角形が存在するための
必要十分条件は,不等式
南海
不等式は![]() に注目すれば
に注目すれば
美樹
はい.まず必要条件を示します.
平面に
![]() があり,
があり,
![]() とする.
とする.
![]() が原点になるように平行移動し,
他の2点の座標が
が原点になるように平行移動し,
他の2点の座標が
![]() であるとする.
このとき
であるとする.
このとき
![]() と
と![]() の大小は,その2乗である
の大小は,その2乗である
![]() と
と![]() の大小と一致します.
の大小と一致します.
また
![]() と
と![]() の大小は,その2乗である
の大小は,その2乗である
![]() と
と![]() の大小と一致します.
の大小と一致します.
そこで![]() の両辺を2乗して差をとる.
の両辺を2乗して差をとる.
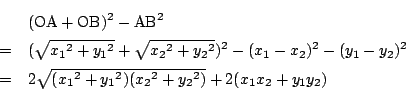
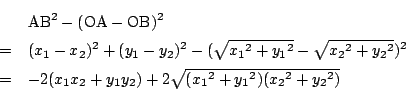
これがともに正であることは
そこで右辺から左辺を引くと
十分条件を示す.
![]() を満たす3正数
を満たす3正数![]() がある.
がある.
![]() を3辺とする三角形が存在することは,
次のように図形的に示される.
を3辺とする三角形が存在することは,
次のように図形的に示される.
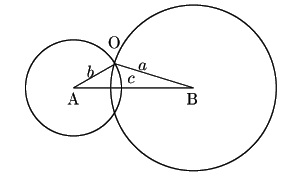
つまり,長さ![]() の線分
の線分![]() をとる.
点
をとる.
点![]() を中心に半径
を中心に半径![]() の円と,
点
の円と,
点![]() を中心に半径
を中心に半径![]() の円をかく.
の円をかく.
![]() は,この2円の中心間の距離cが,
半径の和
は,この2円の中心間の距離cが,
半径の和![]() よりも小さく,
半径の差の絶対値
よりも小さく,
半径の差の絶対値![]() よりも大きいことを意味している.
よりも大きいことを意味している.
よってこの2円は交わる.
交点を![]() とすれば,
とすれば,
![]() となり,
3辺が
となり,
3辺が![]() の
の
![]() が存在した.
が存在した.
これで定理2が示された.□
南海 十分条件の証明は図形に頼った. それも証明にはなっているのだが, 円が交わる条件を無前提に使っている.
美樹 使わずにできるのですか.
南海 図形に頼らない十分条件の証明も試みてみよう. 三角関数を念頭においたものだが,三角関数は使わない.
![]() を満たす3正数
を満たす3正数![]() がある.
このとき,
がある.
このとき,![]() を原点とし,
を原点とし,
![]() とする.
とする.
点
![]() を
を
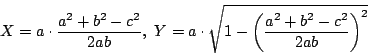
条件![]() は各辺が負でないので
は各辺が負でないので
これから
美樹
あとは
作り方から
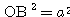 は明らかです.
は明らかです.
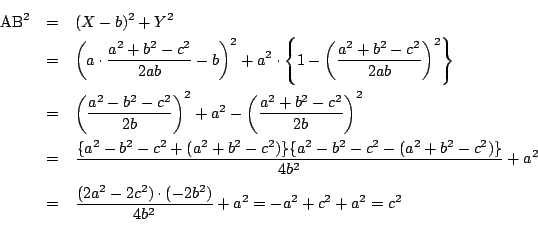
よって![]() を3辺とする三角形が存在した.
□
を3辺とする三角形が存在した.
□
美樹 なるほど.条件を満たす点を実際に構成するのですね.
南海
もちろんこのように![]() を定めたのは,
を定めたのは,
![]() としたとき,
としたとき,
![]() が念頭にあり,それをヒントにしているが,
見つかってしまえば,三角関数とは独立に,定理が示せている.
が念頭にあり,それをヒントにしているが,
見つかってしまえば,三角関数とは独立に,定理が示せている.
三角性の成立条件の不等式のことを三角不等式ともいう.
美樹 三角不等式は, 三平方の定理で特徴づけられる距離から導かれる結果なのですね.
南海 そう. ただし,今度は距離という概念を定義しようとすると, 三角不等式を距離が満たすべき性質の一つとしなければ, 意味のある定義にはならない.
3点が同一直線上にある場合を含めると,
2点
![]() の間の距離
の間の距離![]() というものは,
次の性質をもっている.
平面上の任意の3点
というものは,
次の性質をもっている.
平面上の任意の3点
![]() に関して
に関して
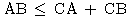
ここでこれをふまえて集合![]() の「距離」という概念を定義しよう.
の「距離」という概念を定義しよう.
定義 1
距離の公理
集合![]() の上に 2変数実数値の写像
の上に 2変数実数値の写像 ![]() が定義されていて、
が定義されていて、
![]() の任意の要素
の任意の要素![]() に対して,
に対して,
![]() が距離の公理とよばれる次の性質を全て満たすなら,
が距離の公理とよばれる次の性質を全て満たすなら,
![]() は
は![]() 上の距離であるという.
上の距離であるという.
美樹
すると
2点
![]() に対して
に対して
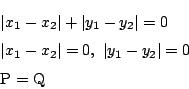
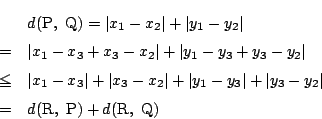
この![]() も距離なのですね.
も距離なのですね.
でもこの距離は,![]() を斜辺とする
直角三角形
を斜辺とする
直角三角形
![]() において
において
南海 そうなんだ. だから逆にいうと,三平方の定理は, 普通の距離,ユークリッドの距離を特徴づけるものなのだ.