 美樹
一般角
美樹
一般角
 美樹
一般角
美樹
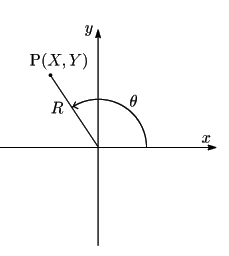
一般角![]() に対して,
その角の
に対して,
その角の
![]() を次のように定める.
を次のように定める.
![]() 平面上の動点
平面上の動点![]() をとる.
をとる.
原点![]() との長さ
との長さ![]() を
を![]() とする.
また
とする.
また![]() 軸の正の方から半直線
軸の正の方から半直線![]() への角が
への角が![]() である.
である.
点![]() の
の![]() 座標が
座標が![]() であるとき,
角
であるとき,
角![]() の三角関数
の三角関数
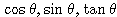 を
を

ただし,![]() のとき三角関数の値は定めない.
また,
のとき三角関数の値は定めない.
また,![]() であるとき,つまり動点
であるとき,つまり動点![]() が
が![]() 軸上にあるとき,
軸上にあるとき,
![]() は定義されないものとする.
は定義されないものとする.
南海 その通り. この定義にもとづいて三角関数の基本性質を導いておこう.
南海 余弦定理は,三角形の辺と内角の間に成り立つ関係と考えられている. またそれに違いはないのだが, 距離と三角関数の基本関係とも見なすことができる.
点
![]() と
点
と
点
![]() をとる.
このとき三平方の定理によって
をとる.
このとき三平方の定理によって
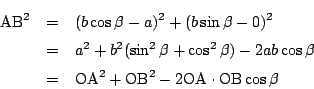
![]() なので,
角
なので,
角![]() は
は![]() から
から![]() にはかっても,
逆にはかってもよく,
にはかっても,
逆にはかってもよく,
![]() で定まる.
で定まる.
美樹 余弦定理って要するに三平方の定理ですか.
南海
![]() なら三平方の定理だ.
もちろんこれは三平方の定理を特別な場合に含む一般的な証明というわけではなく,
三平方の定理をもとに,なす角が直角でない場合に一般化したものだ.
なら三平方の定理だ.
もちろんこれは三平方の定理を特別な場合に含む一般的な証明というわけではなく,
三平方の定理をもとに,なす角が直角でない場合に一般化したものだ.
長さや角は量であり,これらの量は合同な変換によって不変である.
角と角を挟む2つの線分の長さの関係は合同に動かしても変わらない.
したがって平面上の任意の2本の線分![]() と
と![]() と
と
![]() に対して
に対して
平面上の2点
![]() を
を
この2点に関して,三平方の定理から
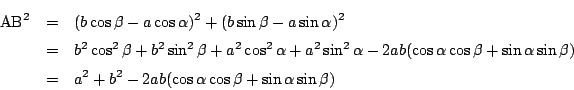
一方余弦定理から
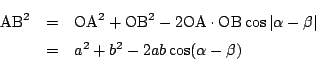
2つを比較して
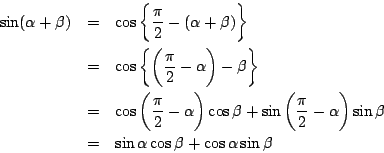
![]() を
を![]() に変えたものを含め
に変えたものを含め

美樹
点![]() を
を![]() 軸上にとって,三平方の定理で余弦定理を導き,
動かしても変わらないことを確認して余弦定理を導いておく.
軸上にとって,三平方の定理で余弦定理を導き,
動かしても変わらないことを確認して余弦定理を導いておく.
こんどは2点を一般の位置にとって,
![]() の長さを,余弦定理と三平方の定理の2通りの方法で書き出す.
の長さを,余弦定理と三平方の定理の2通りの方法で書き出す.
それと等値すると加法定理になる.
南海 そう. だから加法定理は, 三角関数の定義と三平方の定理からただちに導かれる基本定理である,といえる.
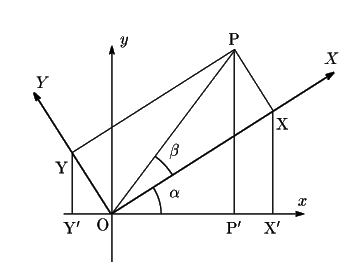 加法定理の証明は次のように余弦定理を使わない方法もある.
加法定理の証明は次のように余弦定理を使わない方法もある.
図のように![]() 座標系と
座標系と![]() 座標系をとる.
座標系をとる.
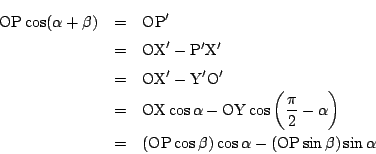
美樹
でも角の向きや点![]() が他の象限にあるときも同様かどうかは,
調べなければならない.
が他の象限にあるときも同様かどうかは,
調べなければならない.
南海 線分にも方向をつけて正負をもたせれば,一般的に成り立つことがわかるのだが, 少し準備がいる.
またこれは,余弦定理を用いてはいないのだが,直角という概念は基本的なもので, 直角は,結局三平方の定理で特徴づけられるので,背景に三平方の定理, ユークリッドの距離があることは,変わらない.