next up previous
次： 定数と変数 上： 方程式と恒等式 前： 方程式と恒等式

文字を用いて式に表す

南海　 数学の教科書や問題には考える数学的な対象を「文字」においたものがたくさんある．

数学の問題を解くということは，文章で記述されたさまざまの数学的な現象を文字を用いて式に表し， 必要な結論を引き出す，ということである． つまり数学的な現象を記述した文章を数式に翻訳し， その数式を操作して結論を示す．

そうでないときもあるのだが，これが問題を解くということの基本だ．

例えば「平面上に2点 $\mathrm{A},\ \mathrm{B}$があり， 線分 $\mathrm{AB}$ 上に点 $\mathrm{P}$ がある．」これは文章である． これを「数学の言葉」に翻訳しなければならない．

この文章を式にするにはどんな翻訳があるか．

史織　

  1. 点 $\mathrm{A}$ を原点，点 $\mathrm{B}$ を $(b,\ 0)$ として， 線分 $\mathrm{AB}$を $xy$ 平面におき，$0 \le t \le b$の実数 $t$ を 用いて $\mathrm{P}(t,\ 0)$ とする．
  2. $0 \le t \le 1$の実数 $t$ を用いて， $\overrightarrow{\mathrm{AP}}=t\overrightarrow{\mathrm{AB}}$ とおく．
等いろいろできます．

南海　 このように「さあ，問題を解こう」とするとき， まず最初に考えなければならないのは「何をどのように文字を用いて表すか」ということである．

これが問題解決の第一歩．適当な文字の導入によって，問題を数学の言葉に翻訳する． 数学が苦手な人は，この「文字の導入による問題の数式への翻訳」が苦手な場合がほとんどである．

数学の対象に文字が使われる場は大きくいって2つある．

  1. 個別のものに名前をつける場合．
    これは文字というより言葉の働きそのものなのだが，数学的対象に名をつけるときには 英語やギリシャ語のアルファベットを用いる．

    ベクトル $\overrightarrow{a}=(1,\ 2)$ といえばこれは数の組$(1,\ 2)$ をベクトルと見なし，これに $\overrightarrow{a}$という名前をつけたのだ． $\bigtriangleup \mathrm{ABC}$ 等もそうだ．

  2. 数を入れる箱としての文字の場合．
    $x^2+ax+1=0$ での文字 $x$ と $a$ は，「数を入れる箱」だ． $x$と$a$のように異なる文字が使われているのは， それが異なる箱であることを示している． そして箱 $a$ に入る数と 箱$x$ に入る数の間に $x^2+ax+1=0$という関係が成り立っていなければならない，ということだ．

後者の文字は変数といわれ，そこに代入されるのが値だ．

人間は，幼い頃3つのリンゴとか3枚の皿のように実際の量の世界にいる． この2つが同じ「3」であることがわかるのは，何歳の頃なのだろう．こうして 量から数への抽象ができるようになる．

量の世界，数の世界もそれぞれに複雜なのだが，さらに数の世界の構造を抽象して 文字の世界に足を踏み入れるのだ．

史織　 それはどういうことですか．

南海　 例えば

\begin{displaymath} 2+1=1+2,\ 3+5=5+3 \end{displaymath}

などが,どのような2つの数でも成り立つ．これを

\begin{displaymath} a+b=b+a \end{displaymath}

と書きあらわすようになるのだ．

史織　 $a$ や $b$ にどんな数を入れても成り立つ，つまり数の加法に交換法則が成り立つ ということですね．

南海　 その通り．そして量や数にもいろいろあるように文字の使われ方にもいろいろある． 量，数，文字にはどんなものがあるかといえば，それぞれ次のような分化が起こる．


量の世界：

　連続量(長さ等)と分離量(個数等)，内包量(1当り量)と外延量 (長さ等)

数の世界：

　自然数，整数，有理数，無理数，実数，虚数，複素数

文字の世界：

　定数，変数，未知数，媒介変数

このように人は徐々に考える世界を広げてきた．
追記(2014.2.7)：　これについてはその後私の考えも少し変わった．『量と数』を見てほしい．

史織　 文字が使われるようになったのはいつ頃からなのですか．

南海　 文字そのものの使用は結構古いが， 文字を用いて個別の数を抽象してとらえ， 色んな変化する数の間の関係を研究する「代数」が生まれたのは古いことではない．

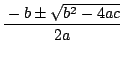例えば，『2次方程式 $ax^2+bx+c=0$ の解の公式が $\dfrac{-b \pm \sqrt{b^2-4ac}}{2a}$ である』 ということは，高校生なら皆知っている．

しかし，このような公式にたどり着くまでには， 多くの人の努力と長い歴史があった．

9世紀のアラビアの数学者アルコワリズミ（Al-Khowarizmi     825 頃）は 『アルジェブル・アルムカバラ（al-gebr w'almuqabala）』という代数学の本を書いた． 「代数（algebra）」の言葉の起源になる本だ．そのなかで平方の出てくる問題を次の6種類に分類し， その解法を研究した（分類は，遠山啓著『数学入門（上)』岩波新書/1959 による）．

  1. 根の平方が根の倍数に等しい
  2. 根の平方が定数に等しい
  3. 根が定数に等しい
  4. 根の平方と根の倍数の和が定数に等しい
  5. 根の平方と定数の和が根の倍数に等しい
  6. 根の平方が根の倍数と定数の和に等しい

当時は今のような「式」がまだなかったのだ．これらは今風に書けば

  1. $x^2=ax$
  2. $x^2=a$
  3. $x=a$
  4. $x^2+bx=a$
  5. $x^2+a=bx$
  6. $x^2=bx+a$

となる．アルコワリズミは文字と等式を知らなかったので，これをすべて文章で書いている． そしてその解き方ももちろん文章で書いている．

例えば，(4)はどのように書いているか． $b=10,\,a=39$ のとき， つまり根の平方とその根の10倍との和が39に等しいという問題の解き方をつぎのように述べる．

『だからこの型についての問は，いいかえるとつぎのようになる． その根の平方に10個の根を加えたとき，その根はいくつか． このような問題の解き方はつぎのようにする．根の平方に加えるべきその根の数を半分にする． いまこの問題では根の数は10である．だから5になる．その数にその数自身をかける． すると25になる．これを39に加えると合計は64になる．その平方根を計算すると8になる． それから根の数の半分の5を引け，残りは3である． これが求めていた数であって，その平方は9である．』

何がいいたいかわかるだろうか．式に書けば次のようになる．

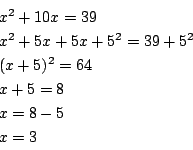
\begin{displaymath} \begin{array}{l} x^2+10x=39 \\ x^2+5x+5x+5^2=39+5^2 \\ (x+5)^2=64 \\ x+5=8 \\ x=8-5 \\ x=3 \end{array}\end{displaymath}

一つ一つの場合についてこのような解き方を述べるのである． 書く方も読む方も大変だ．文字を用いて数式を立てることがどんなにすばらしい発見かわかる．

では先の6つの場合分けはなぜ必要だったのだろうか．

気づいたかもしれないが，0と負の数を知らなかったのだ．0や負数を用いれば，

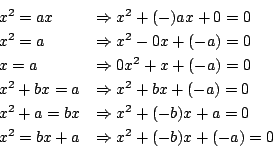
\begin{displaymath} \begin{array}{ll} x^2=ax& \Rightarrow x^2+(-)ax+0=0 \\ x... ...0 \\ x^2=bx+a & \Rightarrow x^2+(-b)x+(-a)=0 \\ \end{array}\end{displaymath}

となり，いづれも

\begin{displaymath} px^2+qx+r=0 \end{displaymath}

になってしまうのだ．

今からおよそ1050年前のことだ．このような時代があって，それから負の数が用いられ， さらにデカルトの時代になって，ようやく文字が一般的に使われはじめ，今に至っている．

このように文字は次のような役割を果たす．

  1. 量や数の間に成り立つ構造や関係を表す．
  2. 変化する量を表すことで動きをとらえる．

みなさんが何気なく勉強していることの中に長い人類の歴史が生きていることが， 言いたかった．文字も大事に使おう．

next up previous
次： 定数・変数 上： 方程式と恒等式 前： 方程式と恒等式
Aozora Gakuen