未知数はわかるのですが,定数と変数の区別がよくわかりません.例えば,
南海
定数と変数は固定的なものではない.動きを止めて考えている方を定数といい,
動かして考えている方を変数(未知数)という.例えば多項式 ![]() がある.
これから
がある.
これから![]() を変数とす る関数
を変数とす る関数
![]() も考えらるが,
も考えらるが,
![]() を変数とする関数
を変数とする関数
![]() も考えられる.
も考えられる.
問題文をよく読み自分で考え方を決めなければならない.1つの問題を考えよう.
2次方程式![]() で,定数
で,定数![]() が
が![]() の範囲にあるとき,
解
の範囲にあるとき,
解 ![]() のとりうる値の範囲を求めよ.
のとりうる値の範囲を求めよ.
これを解くのに,2つの考え方がある.
一つは問題文通り![]() を変数(未知数),
を変数(未知数),![]() を定数としたうえで
を定数としたうえで![]() より
より
![]() の交点が
の交点が![]() でどのような範囲にあるかを見る方法である.
でどのような範囲にあるかを見る方法である.
もう一つはこれを「![]() の1次方程式
の1次方程式
![]() で,解
で,解![]() が
が![]() の範囲にあるとき,
定数
の範囲にあるとき,
定数 ![]() のとりうる値の範囲を求める」とし,
のとりうる値の範囲を求める」とし,![]() の1次関数が
の1次関数が ![]() の区間
の区間![]() で
で![]() 軸と交わる範囲として
軸と交わる範囲として![]() の範囲を出す方法である.
の範囲を出す方法である.
2文字(以上)の関係式があるときどちらを定数と見なし, どちらを変数と見なすかによって異なる方法になる.
この例題を解いてみよう.
史織
やってみます.
方法1
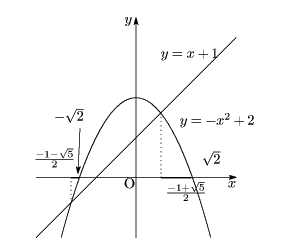 1は
1は ![]() と変形される.これから,2つのグラフ
と変形される.これから,2つのグラフ
史織
第二の方法は, ![]() の1次式と見るのですね.
の1次式と見るのですね.
南海
そうだ.
![]() が求める範囲にあるということは,
が求める範囲にあるということは,![]() で1を満たす
で1を満たす ![]() がとれるという
ことだ.つまり
がとれるという
ことだ.つまり![]() の
の ![]() が存在するような範囲として
が存在するような範囲として ![]() の範囲が定まる.
の範囲が定まる.
![]() が存在する? それは
が存在する? それは ![]() の方程式ということだ.
の方程式ということだ.
それで,定数と変数の見方を変えると,
1は ![]() の1次方程式で
の1次方程式で![]() が定数とも考えられる.このように見れば
が定数とも考えられる.このように見れば
![]() の1次方程式1が
の1次方程式1が![]() に解をもつような定数
に解をもつような定数 ![]() の範囲として,
求まることになる.
の範囲として,
求まることになる.
史織
やってみます.
方法2
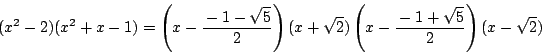
南海
![]() や
や ![]() を変数や未知数,
を変数や未知数, ![]() や
や ![]() を定数と見るのは習慣に過ぎない.要は2つの文字
を定数と見るのは習慣に過ぎない.要は2つの文字
![]() と
と ![]() の間に
の間に![]() の関係が成り立っている,ということだけがある.
いずれを変数とし,いずれを定数とするかは固定されていない.
いくつかの文字の混じった式では,どの文字を固定してどの文字を動かすのかよく考えたい.
の関係が成り立っている,ということだけがある.
いずれを変数とし,いずれを定数とするかは固定されていない.
いくつかの文字の混じった式では,どの文字を固定してどの文字を動かすのかよく考えたい.
史織 いままでは、文字定数は数字の代表だと思ってました。
解いてみての考えなのですが、
例題の方程式を![]() と
と![]() の2変数実関数、
の2変数実関数、![]() の解で第2座標が
の解で第2座標が
![]() の解について解析するというふうに思ったのですが正しいでしょうか.
こうすれば逆手流もすんなりうけいれやすいとおもうのですがいかがですか?
の解について解析するというふうに思ったのですが正しいでしょうか.
こうすれば逆手流もすんなりうけいれやすいとおもうのですがいかがですか?
南海
それはその通りなのだ.ただ「![]() の解」といってもこれは
の解」といってもこれは![]() 平面内の曲線である.
平面内の曲線である.
![]() を満たす点の集合を調べるのに,先に
を満たす点の集合を調べるのに,先に![]() を固定して調べるか,先に
を固定して調べるか,先に![]() を固定して調べるかの違い
だと考えればよい.
を固定して調べるかの違い
だと考えればよい.
また,![]() ,(ただし、
,(ただし、![]() 定数で
定数で![]() )の解の個数を調べるときは,
)の解の個数を調べるときは,
![]() のグラフをax平面に書いて,
のグラフをax平面に書いて,![]() の直線を
の直線を![]() の範囲で動かしていったと
きに,曲線との交点がいくつあるか,という問題として解くことも出来る.
の範囲で動かしていったと
きに,曲線との交点がいくつあるか,という問題として解くことも出来る.
いずれにしても,習慣としてxは変数や未知数を表し,![]() は定数を表す,これは習慣に過ぎない.
2つの文字の間の関係式が大切なのであって,それを満たす点集合を調べる過程で,
先にどちらを止めるか,止めた方をその時点で定数というのだ.
は定数を表す,これは習慣に過ぎない.
2つの文字の間の関係式が大切なのであって,それを満たす点集合を調べる過程で,
先にどちらを止めるか,止めた方をその時点で定数というのだ.