次： 座標幾何のはじまり 上： 座標の方法 前： 座標の方法

座標

南海　 今回は，座標とベクトルを見直し，そのうえで座標平面と関数のグラフの関係や意味を 考えたい．また，空間ベクトルと空間座標についても，いくつか考えよう．

ところでまず平面で座標とは何か．

史織　 平面上の点を $(1,\ 4)$ のように数の組で表すこと，ですか．

しかし極座標というのもあるから，よく考えなければ．

南海　 平面上の点を数の組で表す，ということは正しい．その方法がいろいろある．

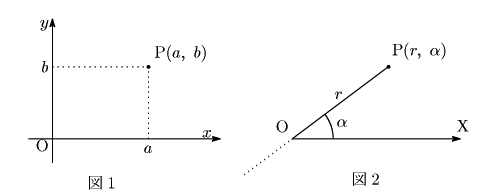
図1のように，2本の数直線をそれぞれの0の点で直角に交わるようにして平面におく． この交点を原点と呼ぶ．

平面上の各点からこれら2本の数直線に垂線を下ろし，それぞれの交点の値が $a$ と $b$ である とすれば，この点に数の組 $(a,\ b)$ を対応させる．するとこの対応は一対一対応で， 平面上のすべての点を数の組 $(a,\ b)$ で完全に表すことができる．

史織　 これが直交座標ですね．

南海　 極座標を説明しよう．

図2のように，基準の半直線 $\mathrm{OX}$ を定める． 始点 $\mathrm{O}$ と点 $\mathrm{P}$ を結ぶ直線が半直線 $\mathrm{OX}$ となす角を定める． つぎにその角の方向から見た $\mathrm{O}$ と $\mathrm{P}$の距離をとる． この距離は負でもよい．これで点 $\mathrm{P}$ に数の組を対応させることができる． これが極座標だ．

この場合も一対一対応だろうか．

史織　 いや，例えば $(1,\ 30^{\circ} )$ と $(1,\ 390^{\circ} )$は同じ点です．

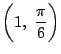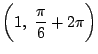南海　 角度を度数法で表すと，これは一般的な「数」ではない．極座標ではやはり弧度法で $\left(1,\ \dfrac{\pi}{6}\right)$や $\left(1,\ \dfrac{\pi}{6}+2\pi\right)$ といわねばならない．

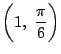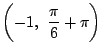いずれにしても表し方は一通りではない． さらに $\left(1,\ \dfrac{\pi}{6}\right)$と $\left(-1,\ \dfrac{\pi}{6}+\pi\right)$ はどうか．

史織　 これも同じ点になります．

南海　 このように極座標では数の組と平面の点は一対一対応ではないが， 数の組によって点が定まることは確かなのでこれも座標といえる．

ついでに言えば複素数の極形式 $z=r(\cos \theta+i\sin \theta)$ 表示では $r$ は $\vert z\vert$ のことなので非負の値にとる約束だ．が，極座標$(r,\ \theta)$で$r$ は任意の実数でよい．

平面の同じ点が直交座標で $(x,\ y)$ ，極座標で $(r,\ \theta)$ となったとすると これらの間には相互の関係式がある．

史織　 はい．

$$x=r \cos \theta ,\ y=r \sin \theta$$

です．

南海　 角は一般角だから当然周期 $2\pi$ で同じ点になる．さらに

$$r \cos \theta=(-r)\cos(\theta+\pi) ,\ r \sin \theta=(-r)\sin(\theta+\pi)$$

なので $(r,\ \theta)$ と $(-r,\ \theta+\pi)$も同じ点を定める．

史織　 ところで今は平面の場合でした．空間の場合，直交座標は習いますが，極座標があるのですか．

南海　 それは次のようにすればよい．

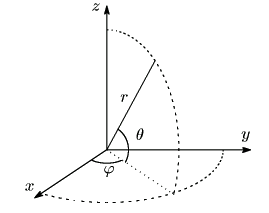このとき

$$x=r \cos \theta\cos \varphi ,\ y=r \cos \theta\sin \varphi,\ z=r\sin \theta$$

になる．

角度は軸から動経の方にはかるとする． また角 $\theta$ は $z$ 軸の正の方からはかる方式もある．

さて，数学の問題に対し，座標の方法によって何ができるか．

1. 図形問題を式に移して考えることができる．
2. 逆に関数を視覚的に考えることができる．

この二つはたがいに関連しているし，実際関連して発展してきた．