次： 関数のグラフ 上： 座標の方法 前： 座標

座標幾何のはじまり

南海　 図形問題を座標で考える．これは高校生諸君にとっては当たり前のことだが， 人間が関数や図形を座標で考えるようになるまでには長い長い道のりが必要だった．

まず前提として

1. 数を一般的な文字であらわすこと．
2. 平面上の点を$(3,\ 2)$ のように数の組であらわすこと．

ができていなければならなかった．

史織　 この二つが準備されれば関数や図形を式にすることができると思いますが．

南海　 ところがそうではなかったのだ．その歴史を少し話そう．

高校で「座標幾何」といっているものは，一般には「解析幾何学」といわれている． この解析幾何学は，座標の考え方で図形問題を解決しようということなのだが， 人間がこのように考えられるまでには上の二つの前提の上に，さらに飛躍が必要だった． 決定的な飛躍をしたのがデカルト(René Descartes,1596-1650)である．

デカルトの時代にすでに文字で考えることは行われていた．

しかし，図形と数を結びつけるとき$a$ とか $x$ とか一つの文字で1次元の量(数直線上の値)を表 わすということが確固としていた． だから， $ab$ といえばこれは $a$と$b$ との積なので，面積を表わすと考えられていた．

すると$ax+by=c$のような式は，面積の和が長さに等しいことを示すことになり， このような式は意味のない式と考えられていた．

史織　 昔の人は数と量(数直線上の長さ)が一体だったのだ．

南海　 その通り．等式は，長さと長さ，面積と面積，体積と体積など次元が同じものどうしが 等しいことを表わすべきであるから，各項の次数が等しい同次式でなければならないと されていた．

フェルマー(Pierre de Fermat,1601-1655)はデカルトと同時代の数学者で，確率論など多くの こととともに，座標，図形の方程式，方程式の表わす図形などを考えはじめた人だが， そのフェルマーでも「図形の等式は同次式でなければならない」という立場自体は ギリシア時代と同じままで何かと不便だった．

一方，方程式の研究などをすすめる代数学においては， 「鶴と亀が合計5匹で，足は合計14本ある．それぞれ何匹いるか」なんかを考え 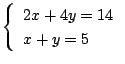$\left\{ \begin{array}{l} 2x+4y=14\\ x+y=5 \end{array}\right.$等を使う．だからもちろん$ax+by=c$という式も意味をもっていた． 同じ式が幾何学では面積の和が長さになるので意味がないとしたのでは， 代数学の演算と幾何学の演算が別のものになってしまう．

ここで飛躍したのが，デカルトだった．デ力ルトがその研究の対象にしたのは， 長さ，面積，体積ではなく，量の抽象としての数そのものであった．彼にとっては， 長さ，面積，体積などの区別はなく，これらはいずれも１つの数で表現されるものだった．

ギリンャ人やフェルマーにとっては，$a，\ b$ はいずれも線分の長さを表わしていたので， $ab$ はこの $a$ と $b$ を2辺とする長方形の面積を意味したわけだが， デカルトはすべて同じ数として考え，$ab$ に別の図形的解釈をおこなった．

1を定めておいて，$a,\ b$ はそれで測った数を表わすとしたうえで， $ab$ を比例式

$$1:a=b:ab$$

における第4項としてとらえた． だから1を表わす長さと $a，\ b$ を表わす長さとが与えられていれば， $ab$ を表わす長さは下左の作図によって求められるものとした．

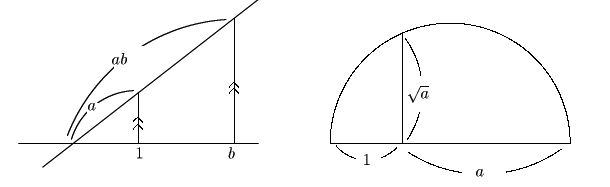さらにまた，同じ理由からデカルト以前の人にとっては， $a$ が線分の長さを表わすと考える 限り， $\sqrt{a}$ は意味をもち得なかったのだが，デカルトは，1を表す長さと $a$ で 表わす長さが与えられた場合，$\sqrt{a}$を表わす長さを上右の図によって作図している．

$$\left(\dfrac{a+1}{2} \right)^2- \left(\dfrac{a-1}{2} \right)^2=a$$

なので，確かに求まる．

このように，デカルトにとっては，線分の長さに代数的な演算を施した結果はまた線分の長さだった． 図形の演算をそれまでの量から独立させて数の幾何として考えはじめたのだ． こうして代数学的演算と幾何学的演算の間には完全な1対1の対応がつき， 代数学におけるすべての方法がそのまま幾何学の研究に使えることになった．

このようなデカルトの飛躍を経て点の座標と線分などのあらわす量が数学の対象と なった．

三つの点 $(1,\ 2),\ (2,\ 3),\ (4,\ 5)$が一直線上にある，ということは相似形の 辺の長さの比を考えれば

$$\dfrac{3-2}{2-1}=\dfrac{5-2}{4-1}$$

という式で表される．ここから文字の考えを用いれば二つの点 $(1,\ 2),\ (2,\ 3)$を 結ぶ直線を

$$\dfrac{3-2}{2-1}=\dfrac{y-2}{x-1}$$

と表そうとすることは，すぐだった．

図形が座標の間の関係式によって表されるという発見は，考えればたいへん大きな発見である．

こうしてデカルトによって今日皆さんが数学IIで習っている直線や円の幾何が始まった．

これらを当然のように使っているが，しかしここに至るには長い歴史と， 幾人かの人による考え方の飛躍があったことを思い起こしてほしい．