次： 定積分の定義 上： 座標の方法 前： 関数のグラフ

ベクトルと座標

史織　 平面座標や空間座標とベクトルの成分表示との関係がはっきりしないのです． 平面の場合どちらも二つの数の組ですが，同じようでもあり違うようでもあります．

南海　 なかなか鋭い疑問だ．では，ベクトルとは何か．

史織　 ベクトルとは，平面，または空間におかれた，方向と大きさ という二つの量によって定まる…,何かです．

南海　 つまり数学の対象ということだ． ベクトルの集合とは，おかれた位置は違っても方向と長さの等しい矢線は 同じものと見なすようにしたときの矢線の集合となる．

ベクトルの定義に座標は関係しているか．

史織　 えーっと，平面上の矢線ですから，どんな座標になっているかは関係ありません．

南海　 一方，どこにおかれているかは関係ないのだから，ベクトルの始点を定まった点 $\mathrm{O}$ にとると，終点が平面上の点として定まる．逆に平面上の点 $\mathrm{P}$ を一つ取るとベクトル $\overrightarrow{\mathrm{OP}}$ が定まる．

このように平面ベクトルと平面上の点は一対一に対応している．

史織　 だから，このとき固定された始点を原点とするような直交座標を一つ入れれば，終点の座標として ベクトルを表すことができる，それがベクトルの成分表示ですね．

南海　 その通り．しかしここからさらに座標というものをもう一度考えることができる．

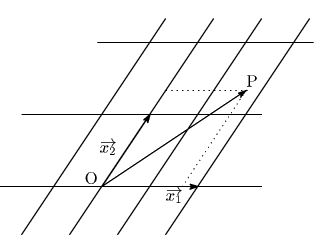
平面で考えよう． たがいに平行でなく0ベクトルでもない二つのベクトル $\overrightarrow{x_1}$ と $\overrightarrow{x_2}$ を定める．また任意の平面上の点 $\mathrm{P}$ をとる． 任意の平面ベクトル $\overrightarrow{\mathrm{OP}}$ は

$$\overrightarrow{\mathrm{OP}}=a_1\overrightarrow{x_1}+a_2\overrightarrow{x_2}$$

と実数 $a_1,\ a_2$ によって一意に表される．

するとこれによって平面上の点 $\mathrm{P}$ と実数の組 $(a_1,\ a_2)$ が一対一に対応する．

史織　 これはまさに座標ですね．

南海　 その通り．これも座標なのだ．図のように平行でない二つのベクトルが定まれば，それによって 平面の点を二つの数の組で表すことができる．

史織　 確かに，平面上の点を数の組で指示することができています．

南海　 $\overrightarrow{x_1}$と $\overrightarrow{x_2}$が大きさが1で互いに直交しているときが いわゆる直交座標なのだ．

史織　 $\overrightarrow{x_1}$の方向を $x$ 軸にし， $\overrightarrow{x_2}$の方向を $y$ 軸にする． そしてそれらのベクトルの終点をそれぞれの数直線の1の点にする．

その結果座標が入りその$xy$ 座標から逆に $\overrightarrow{x_1}$と $\overrightarrow{x_2}$ を表すと

$$\overrightarrow{x_1}=(1,\ 0),\ \quad \overrightarrow{x_2}=(0,\ 1)$$

となるのですね．

南海　 そうだ．

座標と内積

史織　 座標とベクトルの間にこのような関係があるとすると，内積はどのように考えたらいいのでしょうか．

南海　 まず内積の定義は?

史織　 教科書では次のようになっています．

二つのベクトル $\overrightarrow{a},\ \overrightarrow{b}$が ある．二つのベクトルのなす角を $\theta$ とする．このとき

$$\overrightarrow{a}\cdot\overrightarrow{b} =\vert\overrightarrow{a}\vert\vert\overrightarrow{b}\vert\cos \theta$$

と定める． $\overrightarrow{a}\cdot\overrightarrow{b}$ をベクトル $\overrightarrow{a}$と $\overrightarrow{b}$の内積という．

南海　 そうするとベクトルを直交座標の成分で表すとき内積はどのようになるのか．

史織　 ベクトルの成分を $\overrightarrow{a}=(a_1,\ a_2)$ ， $\overrightarrow{b}=(b_1,\ b_2)$ とします．このとき内積は

$$\overrightarrow{a}\cdot\overrightarrow{b} =a_1b_1+a_2b_2$$

です．

証明は二点 $\mathrm{A}(a_1,\ a_2)$ ， $\mathrm{B}(b_1,\ b_2)$ をとり， $\bigtriangleup \mathrm{OAB}$ で余弦定理を適用すると

$$\mathrm{AB}^2=\mathrm{OA}^2+\mathrm{OB}^2-2\mathrm{OA}\mathrm{OB}\cos \theta$$

で， $\mathrm{OA}\mathrm{OB}\cos \theta=\overrightarrow{a}\cdot\overrightarrow{b}$ なので

$$(a_1-b_1)^2+(a_2-b_2)^2 =a_1^2+b_1^2+a_2^2+b_2^2-2\overrightarrow{a}\cdot\overrightarrow{b}$$

となります．これから内積の成分表示が得られます．

南海　 そういうことだ．ところで，逆に

$$\overrightarrow{a}\cdot\overrightarrow{b} =a_1b_1+a_2b_2$$

を内積の定義とすれば，上の余弦定理の式を逆にたどって

$$\overrightarrow{a}\cdot\overrightarrow{b} =\vert\overrightarrow{a}\vert\vert\overrightarrow{b}\vert\cos \theta$$

が得られる．つまり二つの定義は同値ということだ．

史織　 二つの定義のうち一方は座標に関係なく，一方は座標の成分で表されます． 一方は座標の入れ方に関係するのに，一方は関係しません．なんかおかしいです．

南海　 このおかしさに気づくのは高校範囲を超えているのだが，質問が出たので答えておこう． 実は

$$a_1b_1+a_2b_2$$

は，座標を入れればこのようにかけるというだけで，その本質は座標とは関係ないのだ．

史織　 では何でしょうか．

南海　 それはベクトルの大きさだけを用いて定義されるのだ． ベクトル $\overrightarrow{a}$ の大きさを絶対値の記号を使って $\vert\overrightarrow{a}\vert$ と表そう．

すると内積は，

$$\overrightarrow{a}\cdot\overrightarrow{b} =\dfrac{1}{2}\left... ...errightarrow{a}\vert^2-\vert\overrightarrow{b}\vert^2 \right\}$$

と表される．

史織　 確かにこれは，ベクトルの大きさしか使っていないし座標とは無関係ですね．

直交座標を入れて，その成分を用いれば確かに

$$\dfrac{1}{2}\left\{\vert\overrightarrow{a}+\overrightarrow{b... ...}\vert^2-\vert\overrightarrow{b}\vert^2\right\} =a_1b_1+a_2b_2$$

になります．

南海　 ま，このあたりは大学生になって線形代数を学び，二次形式と線形代数辺りを学んだときに 思い出してくれればよい．

さてこのように座標とベクトルは一体のものなので，図形関連の問題では両者を いったりきたりして考えるとよい．いくつかの例で考えよう．