次： 平面上の直線(その一) 上： 平面上の直線 前： 平面上の直線

二つのベクトルの平行条件

南海　 まず $\overrightarrow{\mathrm{O}}$ でない二つのベクトル $\overrightarrow{a}=(a_1,\ a_2)$と $\overrightarrow{b}=(b_1,\ b_2)$ が平行である条件から考えよう．

史織　 平行ということは方向が同じで大きさは違ってもよいということなので， 0でない実数 $t$ で

$$(b_1,\ b_2)=t(a_1,\ a_2)$$

となるものがあることと同値です．

$\overrightarrow{a}$と $\overrightarrow{b}$が平行， つまり $b_1=ta_1,\ b_2=ta_2$なる $t$ があるとします．このとき

$$a_2b_1=ta_2a_1,\ a_1b_2=ta_1a_2$$

なので， $a_1b_2-a_2b_1=0$ です．

逆に $a_1b_2-a_2b_1=0$とします．

$a_1=0$なら$a_2\ne 0$ なので$b_1=0$ となり $\overrightarrow{a}$と $\overrightarrow{b}$は平行， $a_2=0$ のときも同様．

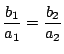$a_1a_2\ne 0$ とする． このとき $\dfrac{b_1}{a_1}=\dfrac{b_2}{a_2}$となる．この比の値を $t$ とすると，

$$(b_1,\ b_2)=t(a_1,\ a_2)$$

したがって

$$a_1b_2-a_2b_1=0$$

が求める必要十分条件である．

南海　 よろしい．最近入試問題にもこのような基本的な問題が出るので，日頃から基本事項を自分で 証明できるようにしていこう．

さて平面上の直線の式について考えよう．それは二つの異なる方法で求まる．