まず第一の方法だ.平面上の二点
![]() がある.
このとき直線
がある.
このとき直線 ![]() の式をベクトルを用いて求めよ.
の式をベクトルを用いて求めよ.
史織
ベクトルですか.直線 ![]() 上の点を
上の点を
![]() とおく.この
とおく.この ![]() と
と ![]() が
満たす式を求めればよいのですね.平行条件をうまく使えないかな.
が
満たす式を求めればよいのですね.平行条件をうまく使えないかな.
二つのベクトル
これを計算すると
南海 そうだ.これは昔どおり傾きを求めてから導く直線の式と同じだろう.
![]() のとき
のとき ![]() はまた
はまた
これをほんの少し違う形で導こう.
史織
![]() 式を成分で書くと
式を成分で書くと
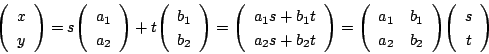
これより
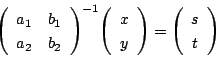
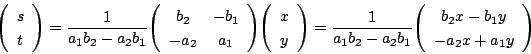
したがって ![]() より
より
あっ.先ほどの式 ![]() と同じだ.
と同じだ.
南海
式が同じになるのは当然なのだが,なかなかおもしろい.行列を習っていない人は, ![]() と
と ![]() を
未知数として連立一次方程式を解いたと考えればよい.
を
未知数として連立一次方程式を解いたと考えればよい.