


次: 定積分の定義
上: 定積分の定義
前: 定積分の定義
史織 図書館で参考書を見ていたら
が,微積分の基本定理と書いてありました.
でも高校の教科書では,
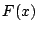 が
が 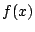 の原始関数のとき
の原始関数のとき
と定める.
となっています.
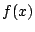 の原始関数とは微分すれば
の原始関数とは微分すれば 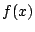 となる
関数のことですから,
となる
関数のことですから, が成り立つのは当然で,
「基本定理」というようなことではないはずです.
が成り立つのは当然で,
「基本定理」というようなことではないはずです.
南海 なるほど.教科書にはどのように書いてあるのか見てみよう.
手元にあるのは「数研出版」の1997年版の教科書だ.次のような流れになっている.
- 区間
![$[a,b]$](images/img876.png) で常に
で常に 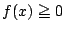 のとき,
区間
のとき,
区間![$[a,x]$](images/img878.png) で
で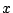 軸と
軸と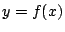 のグラフ,
および
のグラフ,
および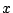 軸の点
軸の点
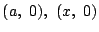 を通る2直線で囲まれた図形の面積を
を通る2直線で囲まれた図形の面積を 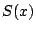 とする.
このとき
とする.
このとき 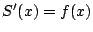 であることを示す.
このことは
であることを示す.
このことは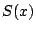 が
が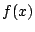 の原始関数の一つであることを意味するので,
の原始関数の一つであることを意味するので,
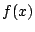 の任意の原始関数
の任意の原始関数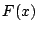 を用いて
を用いて
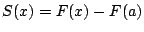 と表される.
と表される.
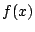 の
の 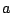 から
から 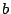 までの定積分を
までの定積分を
で定義する.(以上数学II)
- 区間
![$[a,b]$](images/img876.png) を
を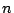 等分して
等分して
とし,
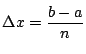 とおくとき,
とおくとき,
が成り立つ(数学III).
このようになっている.これは新しい課程でも変わらない.
史織
定積分の定義が(2)なので,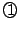 が成り立つのは当然です.
一体なぜ
が成り立つのは当然です.
一体なぜ  を基本定理というのでしょうか.
を基本定理というのでしょうか.
南海 結論をいえば,この教科書の定義が正確ではないのだ.
このように定積分を定義するのは日本の高校教科書くらいなものだ.
それも前回の高校課程の改訂でこうなった.
かつては正しく定義されていた.
Aozora Gakuen
が
の原始関数のとき
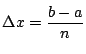 とおくとき,
とおくとき,
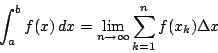
![]() が成り立つのは当然です.
一体なぜ
が成り立つのは当然です.
一体なぜ ![]() を基本定理というのでしょうか.
を基本定理というのでしょうか.