関数![]() は閉区間
は閉区間 ![]() で連続とする.
で連続とする.
史織 どのように定義すべきなのでしょうか.
南海 今手元に1969年の日本書院の教科書がある. 数学IIBと数学III では区間の分割が等分か任意の分割かが違うのだが, 本質的に同じなので,ここでは数学III の定義を紹介しよう. 次のように書かれている.
関数
は閉区間
で連続とする.
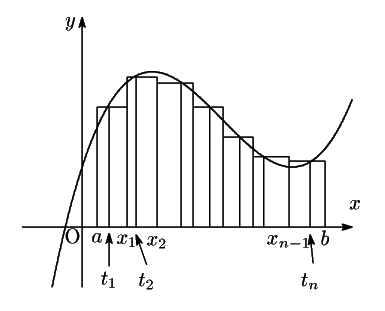
この区間を図のように

個の点
をとって,和
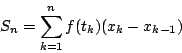
を作る.すべての小区間の長さが,いずれも0に近づくように
この極限値を,関数を限りなく大きくするとき,
の点のとり方にかかわらず,和
は一定の極限値に近づくことが知られている.
の区間
における定積分といい
で表す.
史織 区分求積法に出てくる和の極限値が定積分の定義なのですね.
南海 1969年には正しく書かれていた. 連続なら収束することは,証明はないが正しく指摘されている.
さらに,1984年に初版が出た『問題新集 微分・積分基本500選』(科学新興社)では, まとめに次のように書かれている.
とする.
を区間
で定義された関数とする.分割
により,を
個の小区間
に分ける. 各小区間に属する任意の点をとる. また,
に対する小区間の幅
の 最大値を
で表す.
極限値
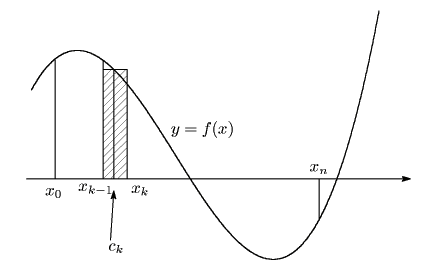
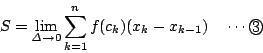
が存在するとき, ![]() は
は ![]() で積分可能であるといい,
で積分可能であるといい,
と定める.
南海 これが正確な定積分の定義だ.
この和
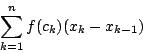
この定義では「 ![]() が存在するとき」と書かれているがそれは
が存在するとき」と書かれているがそれは
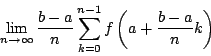
史織 ![]() を小区間の端点にとるのですね.
を小区間の端点にとるのですね.
そうすると,定積分の定義というのは,
![]() のグラフと
のグラフと ![]() 軸で囲まれた図形の
軸で囲まれた図形の ![]() 軸の上にある部分の面積を
軸の上にある部分の面積を ![]() で,
下にある部分の面積を
で,
下にある部分の面積を![]() でとり加えたもの,を意味するのですね.
でとり加えたもの,を意味するのですね.
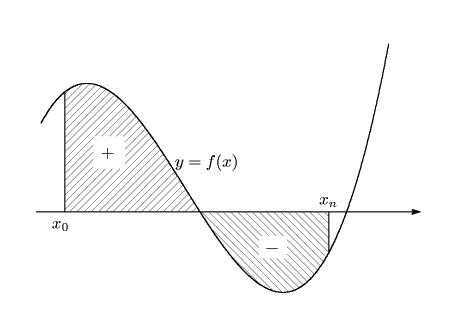
南海 その通りだ.積分というのは歴史的にも求積法から来ているのだ.