


次: 同型定理と演算
上: 自然数と数学的帰納法
前: ペアノの公理
ここで「昇列」を定義する.
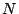 の部分集合
の部分集合 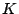 で
で
が成り立つとき 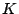 を「昇列」という.
を「昇列」という.
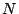 の要素
の要素 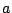 を含むすべての昇列の共通部分を
を含むすべての昇列の共通部分を 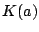 とする.
これは
とする.
これは 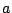 からはじめて
からはじめて 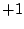 の規則で作られた要素だけの集合である.
の規則で作られた要素だけの集合である.
定理 1
証明
- 1を含む任意の昇列
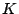 に対し,
に対し,
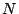 において
において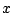 に
に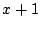 を対応させる規則を
を対応させる規則を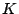 に制限した規則を考える.
定義より,
に制限した規則を考える.
定義より,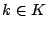 のとき
のとき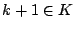 であるから,
これは
であるから,
これは 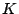 の要素
の要素 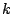 に
に 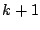 を対応させる規則となる.
この対応の規則によって,
を対応させる規則となる.
この対応の規則によって, 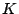 は 自然数の公理(i)(ii)(iii)(iv)を満たす.
は 自然数の公理(i)(ii)(iii)(iv)を満たす.
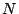 の最小性から
の最小性から 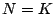 である.よってまた
である.よってまた 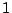 を含む昇列はすべて
を含む昇列はすべて 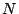 に一致する.
に一致する.
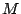 は
は 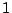 を含む昇列である.ゆえに(1)から
を含む昇列である.ゆえに(1)から 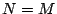 .
.
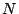 において,
において,
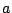 にはじまり
にはじまり 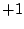 の操作を繰り返して
の操作を繰り返して 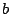 に至る系列はただひとつである.
二つあれば,そのいずれかの系列を定めその中にのみ存在する要素を
に至る系列はただひとつである.
二つあれば,そのいずれかの系列を定めその中にのみ存在する要素を 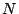 から取り除いても,
から取り除いても,
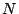 は
は 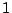 を含む昇列となり
を含む昇列となり 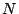 の最小性に反するからである.
の最小性に反するからである.
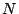 の要素
の要素 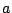 で
で 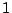 でなく,
しかも
でなく,
しかも 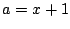 となる要素
となる要素 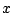 が存在しない要素の集合を
が存在しない要素の集合を 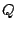 とする.
とする.
とする.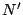 の任意の要素
の任意の要素 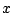 に対して
に対して 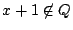 つまり
つまり 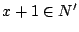 である.
ゆえに
である.
ゆえに 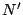 は
は 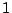 を含む昇列であるから
を含む昇列であるから 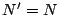 .つまり
.つまり 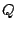 は空集合であり,
は空集合であり,
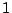 以外で直前の要素の存在しない要素はない.
以外で直前の要素の存在しない要素はない.
次に 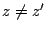 かつ
かつ 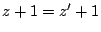 となるものがあるとする.二つの系列
となるものがあるとする.二つの系列
が存在し,系列の唯一性に反する.ゆえに直前の要素はただひとつである.
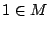 なら
なら 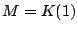 なので
なので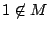 とする.
とする.
とおく.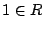 なので
なので 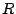 は空でない.
は空でない.
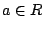 であるが
であるが 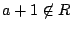 であるような要素
であるような要素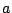 が
が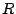 に存在する.
なぜなら,もしなければ
に存在する.
なぜなら,もしなければ 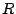 が
が 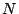 自身になる.
ところが
自身になる.
ところが 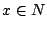 に対して
に対して
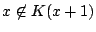 だから
だから
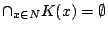 である.
つまり
である.
つまり
となって 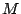 が空集合になるのである.
が空集合になるのである.
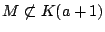 なので
なので
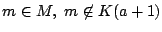 が存在する.つまり
が存在する.つまり
となり 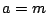 ,つまり
,つまり 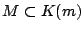 となる
となる 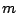 が存在した.
が存在した.
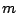 と
と 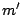 と二つあれば
と二つあれば 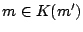 かつ
かつ 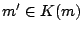 となり,
となり,
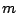 から
から 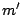 をへて
をへて 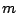 にいたる系列ができる.
にいたる系列ができる.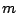 から
から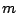 にいたる系列が2つでき,
系列がただ一つであることに反する.□
にいたる系列が2つでき,
系列がただ一つであることに反する.□
このように構成された集合 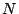 の要素は
の要素は
という形をしている.これを表記の簡単のために
と書くのである.
史織
なぜ先の定理が数学的帰納法の原理 とよばれるのですか.
南海
数学的帰納法とは次のような証明方法であった.
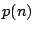 を自然数
を自然数  に関する条件とする.
に関する条件とする.
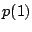 が成立する.
が成立する.
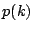 が成立するなら
が成立するなら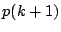 が成立する.
が成立する.
- (1), (2)より, すべての自然数
 に対して
に対して 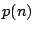 が成立する.
が成立する.
南海
数学的帰納法を言いかえると,条件 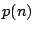 の真理集合,つまり
の真理集合,つまり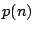 が真となるような
が真となるような の集合が,
自然数全体であることを示すということになる.
の集合が,
自然数全体であることを示すということになる.
史織
集合の記号を用いると条件 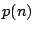 の真理集合
の真理集合 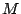 は
は
となります.
自然数の性質によって,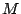 が
が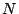 と一致するのですね.
と一致するのですね.
数学的帰納法の(1)は 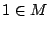 を示している.(2)は
を示している.(2)は 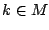 なら
なら 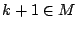 を示している.
つまり
を示している.
つまり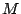 は1を含む昇列なので
は1を含む昇列なので
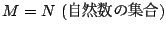 である.
条件が成立する
である.
条件が成立する  の集合
の集合 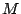 が自然数全体となり,
すべての自然数
が自然数全体となり,
すべての自然数  でなり立つ,つまり(3)の成立がわかる,
でなり立つ,つまり(3)の成立がわかる,
これが数学的帰納法です.
南海
そのとおり.
自然数の集合というのは,
「1があって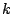 が要素であれば
が要素であれば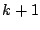 も要素である」ような集合でいちばん小さいもの,
として特徴づけられる.
も要素である」ような集合でいちばん小さいもの,
として特徴づけられる.
このように数学的帰納法が証明の方法として成立するのは,自然数の性質が土台にあるからである.



次: 同型定理と演算
上: 自然数と数学的帰納法
前: ペアノの公理
Aozora Gakuen
![]() の部分集合
の部分集合 ![]() で
で
![]() は,次の性質をもつ.
は,次の性質をもつ.
![]() かつ
かつ ![]() となるものがあるとする.二つの系列
となるものがあるとする.二つの系列
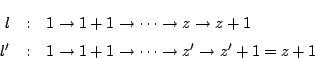
![]() なので
なので
![]() が存在する.つまり
が存在する.つまり
![]() の要素は
の要素は
![]() を自然数
を自然数 ![]() に関する条件とする.
に関する条件とする.
![]() の真理集合,つまり
の真理集合,つまり![]() が真となるような
が真となるような![]() の集合が,
自然数全体であることを示すということになる.
の集合が,
自然数全体であることを示すということになる.
![]() の真理集合
の真理集合 ![]() は
は
![]() が
が![]() と一致するのですね.
と一致するのですね.
![]() を示している.(2)は
を示している.(2)は ![]() なら
なら ![]() を示している.
つまり
を示している.
つまり![]() は1を含む昇列なので
は1を含む昇列なので
![]() である.
条件が成立する
である.
条件が成立する ![]() の集合
の集合 ![]() が自然数全体となり,
すべての自然数
が自然数全体となり,
すべての自然数 ![]() でなり立つ,つまり(3)の成立がわかる,
でなり立つ,つまり(3)の成立がわかる,
![]() が要素であれば
が要素であれば![]() も要素である」ような集合でいちばん小さいもの,
として特徴づけられる.
も要素である」ような集合でいちばん小さいもの,
として特徴づけられる.