次： 実数とは何か 上： 自然数と数学的帰納法 前： 数学的帰納法

同型定理と演算

南海　 自然数の公理を満たすものがいくつもあっては困る． しかし実は一つしかないことが示される．

定理 2

自然数の集合$N$ はすべて同型である．つまり二つの自然数の集合 $N$ と $N'$ があるとする． $N$と $N'$ のあいだの1:1対応 $f(x)$ で

1. $f(1)=1$
2. $f(x+1)=f(x)+1$

となるものがある．

証明      $N_n=\{1,\ 2,\ \cdots ,\ n\}$の $N'$ への埋め込み（中への同型対応） $f_n(x)$ を数学的帰納法で定める．

1. $n=1$ のとき $f_1(1)=1$ とする．
2. $f_k(x)$ が定まったとき
   
   $$f_{k+1}(x)=f_k(x) \ ( x=1,\ 2,\ \cdots ,\ k),\ f_{k+1}(k+1)=f_k(k)+1$$
   
   
   とする．一対一であることは明らか．

つまり，次のように$f_n(x)$を構成する．

$f_k(x)$は集合{1,2,…,k}から$N'$への写像．これができたとき，これを用いて{1,2,…,k,k+1}から$N'$への写像 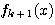 を，1,2,…,kに対しては$f_k(x)$と同じk+1に対して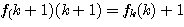で定める．

この $f_n(x)\ (n=1,\ 2,\ 3，\cdots)$ に対して

$$f(x)=f_x(x)\ \ x \in N$$

と定める．作り方から $f(N)$ は $N'$ における $1$ を含む昇列である．

$$∴ \quad f(N)=N'$$

このとき

$$f(x+1)=f_{x+1}(x+1)=f_x(x)+1=f(x)+1$$

であるから題意を満たしている．□

自然数の和・積

南海　 この自然数の集合には，和と積という演算が定義される．

和の定義 $x,\ y\in N$ に対して， $x+y$ を作る演算を次のように定める．

1. $y=1$ なら $x+y=x+1$
   
2. $y>1$のとき
   
   $$x+y=(x+(y-1))+1$$
   
   

このとき $x+y$ がただ一通りに決まり次の性質を持つ．

1. 結合法則： $(x+y)+z=x+(y+z)$
2. 交換法則：$x+y=y+x$

南海　 これはゆっくりやればできるので，やってみてほしい．

およそこのようにして，自然数は厳密に定義される． それから有理数が構成され，実数，複素数と進んでいくのだ．

史織　 このようにある意味では単純に定義される自然数が，因数分解をもち，素数というものがあり， いろんな未解決の問題があるというのは不思議です．

南海　 まったく同感．