ここで確率変数![]() を
を![]() 回の試行中そのことが起こる回数とする.
回の試行中そのことが起こる回数とする.
この確率分布を二項分布という.
史織 これって独立試行の確率そのものではありませんか. この確率は標本空間は何ですか.
南海
![]() 回の試行でそのことが起これば○,起こらなければ×,とすると,
回の試行でそのことが起これば○,起こらなければ×,とすると,
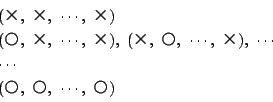
史織
そうか.![]() 回起こる各々の確率が
回起こる各々の確率が![]() でそれが
でそれが
![]() 通りあるから,確率が
通りあるから,確率が
![]() なのだ.
なのだ.
南海
この確率分布は,二項定理
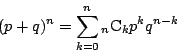
このとき,起こる回数の期待値 ![]() は
は
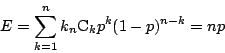
これを示すために二項定理は![]() と
と![]() の恒等式なので,これを
の恒等式なので,これを![]() で微分して
で微分して
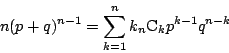
この係数比較から
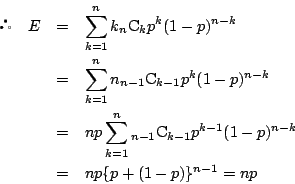
二項分布に係わる最近の問題を紹介しよう.
![]() を3以上の自然数とする.スイッチを入れると等確率で赤色または青色に輝く電球が横一列に
を3以上の自然数とする.スイッチを入れると等確率で赤色または青色に輝く電球が横一列に![]() 個並んでいる.
これらの
個並んでいる.
これらの![]() 個の電球のスイッチを同時に入れたあと,左から電球の色を見ていき,色の変化の回数を調べる.
個の電球のスイッチを同時に入れたあと,左から電球の色を見ていき,色の変化の回数を調べる.