南海 そのとおり.量のもつべき性質を考えるとき,助けになっているのは実直線だ.基点からの長さが量のいちばん簡明なモデルになる.実直線は,目盛りを打てば,つまり座標を入れれば,数にそのまま対応する.
一般的に言って,量としての把握の深まりは,つねに数の深まりと一体であった.だから,量が現実の物理的な世界のことであるとして,それを量としてつかむときに,そこには必ずそれを写し取る数があった.
逆にいうと量は現実世界と数を媒介するものだ.媒介するものとして,量の条件で考えたような構造をもっている.しかしそれはただちに数の構造である.
一方,数学の世界もまた物理世界から抽象化された単なる言葉などというものではなく,豊かで深い世界である.何らかの数学的実在,あるいは数学的現象の実在はまちがいない.
太郎 人間のたどってきた長い歴史を考えさせられます.
南海 同感.さて,『知識は永遠の輝き』というブログの2010-03-30付「 量とは-3- 負の量」に次の記事があった.
また青空学園数学科では次のような記載があります。 「速度と時間の場合には確かに負数と負数の積は正数だが,それでなぜすべての量で成立することが示せたのかという問題もある.量を数化すると同じ計算法則を満たす.だから計算法則の方から証明しておけば,すべての量で成り立つ.この道を通らないと,個別の量を超えた量一般での証明は難しい.」
これは少し論理が甘いでしょう。「量を数化すると同じ計算法則を満たす」ということが全ての量で成り立つことが示されないと、上記の論理は完全ではないからです。でもそれは個別の量で個別にしか確認できないことです。そもそも負値を取らない量だってあるのですから。
これはまったくその通りである.
最初に『量と数』を書いたのは,2008.2.18であった.その後,2008.9.10から『解析基礎』「まえがき」「第1章」を作り,2009.2. 17に『解析基礎』終章までを仕上げた.その過程でこちらの考えも深まった.『解析基礎』のなかで
人間は長い長い時をへて,量の認識に至った.概念として量が先行するとはいえ,量の認識に数は不可欠である.量と数は互いに相手の展開を促しながら相互に発展してきた.現代においては,数は公理的に構成され,構成された数によって現実の世界の諸々を近似する.量とは現実と数を媒介する概念である.と書いた.確かに最初の『量と数』の書き方では,「量を数化すると同じ計算法則を満たす」ことがすべての量で成り立つことは証明されない,というのは正しい.事実は,数が先に準備されていて,それによって現実を近似して量としてつかむのである.つかまれた量がその数の法則を満たすのは,したがって当然である.数を離れて「すべての量で成り立つ」ことがいえるのではない.
数学の立場からは,量は数による現実の近似的把握の結果,つかまれることである.それ自体で数から独立に客観的に存在するのではない.量が認識されるとき,数による近似的把握が行われている.うまく近似できないとき,別の数体系が必要となるかも知れない.正値だけの数の集合が必要かも知れない.だから私のもとの文章で「すべての量で成り立つ」としたところは,「一つの数体系で近似するかぎりその量においては成り立つ」としなければならない.
太郎 現実を分節して切りとってつかむのが言葉であると言われます.これから言うと,数も言葉ですね.
南海 成長とともに身につける言葉を母語という.これからすると,数は第二の母語であるといえる.数があってはじめて,比べうる何かが量としてつかまれる.比べうる何かは先にあるが,それはまだ量ではない.量としてつかむ前提は数である.そして,同じ数でつかまれた量は同じ構造をしている.
太郎 青空学園でも数の公理的な構成についてはいくつか読んだことがあります.
南海 これまで青空学園で数の構成について考えてきたのは次の四つである.
『数学対話』の「 自然数と数学的帰納法」
『数論初歩』の「 存在と構成」
前者で自然数の構成を,後者で自然数,整数,有理数の公理的な構成を行った.
数えるということから自然数が定義される.そこではペアノの公理によって自然数を定義した.『整数の基本』では自然数を次のように定義した.
これを公理に定式化したのがペアノの公理であり,数えるということの本質をついている.『数論初歩』では次の定義を採用した。からはじめて,「1たす」という操作だけで作られる数の集合を自然数の集合といい,その要素を自然数という.
これは集合をもとに考えているので,ペアノ自身の定義とは異なることになるのだが,一般的には分かりやすい。
自然数からはじめて,整数,有理数と順次構成した.そこで用いた方法はいずれも,それまでにできている数の世界の二つの数の組![]() の集合を考え,その同値関係による商集合として定義した.
の集合を考え,その同値関係による商集合として定義した.
太郎 それぞれを読んでみました.いろいろな計算規則も,公理系から証明できそうです.
南海
このような公理系のなかでは,かつて量を用いて教えた
負数×負数=正数であることや,分数のかけ算では分子と分子,分母と分母をかければよいことなども,証明できる.
太郎 確かに.しかし,量による説明の方がよくわかります.計算の公理からの論証は,これでないといけないという必要条件という感じですが,量による説明は,必要十分な感じがします.
南海 確かにそうなのだ.そこに,歴史的に積みあげられてきた数学と,子どもたちに自分で確認できるところから積みあげて数を伝える数学教育とを,どのように統一しつつ分離するかという問題があり,かけ算の積の順の問題のように,40年間解決していない課題もまた多く残されている.この問題がもういちど最後に考えよう.
さて実数については,次のところで述べてきた.
『数学対話』の「 実数とは何か」
『解析基礎』の「 実数の構成」
実数の集合![]() を次の公理によって定まる構造をもつものとして定義した。
を次の公理によって定まる構造をもつものとして定義した。
今後この対話をふまえて『解析基礎』を改訂したいと考えているが,第1版ではこのようなものとして実数を定義した.
太郎 この公理を満たすような集合が本当にあるのか,という問題が出てくるように思います.
南海 それを有理数から構成するうえでは,カントールの方法とデデキントの方法がある.『解析基礎』ではそれを実行し,そのうえでいくつかの基本性質を証明した.
そこにも述べられているように,基本列(コーシー列)が極限をもつことを「完備性」という.デデキントとカントールの二つの方法は同値で,いずれにおいても実数はこの意味で完備である.そして実数とは「数列が収束するための必要十分条件は基本列(コーシー列)であることである」が満たされる集合であることを示した.
太郎 基本列というのは
数列ということでした.で,任意の正数
に対して,番号
で,
のとき
となるものが存在する.
有理数や実数からなるこのような数列は,実数の中であればつねに極限をもつ.これが実数の完備性ですね.
南海 そうだった.これらは,自然数からはじめて順次数を構成してゆくものであり,実際に19世紀の西洋でなされてきた経過にしたがっている.
そのために,まだ定義していなかった量を定義し,先に考えてきた量への要請を満たす量は,すべて実数で捉えることが出来ることを示そう.
量とは「もの」に付随する,比較することや一定の操作をすることができるような何らかのことである.人間は長い時間と歴史を経て,比較するための普遍単位を獲得した.例えば,長さについていえば,フランス革命を経てメートル原器が定められた.つまり1mの確定である.その後,地球の周の長さから定めたり,ある種の光線の波長から定めたりと,観測技術の発展に応じて定め方は変わってきた.が,単位となる量を普遍的に定め,それに数値をかけることで,量を定めてきた.
太郎 その数値というのは,実数ですね.
南海 実際はそうなのだが,論理的な順として,いまは単に数として考える.また,かつてハミルトンは四元数を発見し,それによって物理的な現象を記述しようとした.また電気などの取り扱いでは複素数が使われることもある.これらの場合は量自体も多元的なものになり,量への要請を満たすとはかぎらない.
数![]() は,準備された数のある部分集合とし,和と積が定義されそれに関して閉じ,乗法の単位元を含むとする.このとき,単位と呼ばれる
は,準備された数のある部分集合とし,和と積が定義されそれに関して閉じ,乗法の単位元を含むとする.このとき,単位と呼ばれる![]() と数を用いて,形式的な次の集合
と数を用いて,形式的な次の集合![]() を考える.
を考える.
太郎
これは単位を用いています.単位は単位量をもつ量です.ですから量そのものの概念を定義したとは思えないのですが.また![]() は
は![]() と
と![]() の積ですか.
の積ですか.
南海
数学として量を定義するときは,一定の公理で定義される構造を定めるのだ.その意味で,単位![]() そのものは無定義用語でよい.
そのものは無定義用語でよい.![]() もまた形式的な結合と考えてよい.そのモデルとしては,現実の量と同じく,単位の量をある数
もまた形式的な結合と考えてよい.そのモデルとしては,現実の量と同じく,単位の量をある数![]() だけ倍したものでとることが出来る.
だけ倍したものでとることが出来る.
南海 この集合に次のような構造を入れる.
南海 これを公理Iとしよう.
太郎 これだけですか.量に積はないのですか.
南海 積は新たな量を生みだす.
太郎 そうか.長さと長さの積は面積という別の量になる.
南海 これだけではもとより量の前提的な定義である.
これを公理IIとしよう. 公理I,IIの成り立つ集合を量空間といい, 公理Iのみ成り立つ集合を非アルキメデス量空間という.
量空間とは,比較可能性,和差可能性,計測可能性をみたす量の集合であるといえる.このとき次の基本的事実が成り立つ.
証明
1)
![]() を
を![]() で定めることにより,
で定めることにより,![]() と
と![]() は一対一に対応する.
は一対一に対応する.
![]() で
で![]() に順序を入れると,
に順序を入れると,![]() は全順序集合になる.埋め込みを示すので,集合
は全順序集合になる.埋め込みを示すので,集合
したがってはじめから,![]() は全順序加法群でアルキメデスの公理が成り立つものとしてよい.
は全順序加法群でアルキメデスの公理が成り立つものとしてよい.
2) ![]() の数
の数![]() をとる.任意の数
をとる.任意の数![]() に対して
に対して
3)
![]() の部分集合
の部分集合![]() を
を
4)
![]() に最小の元が存在する場合.
に最小の元が存在する場合.
![]() の元
の元![]() に対し,
に対し,
![]() となる自然数
となる自然数![]() をとる.
をとる.
![]() で
で![]() であるから,もし
であるから,もし![]() なら
なら![]() の最小性と矛盾.よって
の最小性と矛盾.よって![]() となる.
となる.![]() は単射でありこれによって
は単射でありこれによって![]() は自然数に埋め込まれた.その結果
は自然数に埋め込まれた.その結果![]() は整数に埋め込まれる.この対応によって順序が保存されることの証明は難しくない.それは略する.
は整数に埋め込まれる.この対応によって順序が保存されることの証明は難しくない.それは略する.
5)
![]() に最小の元が存在しない場合.
に最小の元が存在しない場合.
まず,![]() は1を含む加法群であるから整数を含むとしてよい.この整数はそのまま自然に大小関係を保存して実数体の中に埋め込まれているとする.
は1を含む加法群であるから整数を含むとしてよい.この整数はそのまま自然に大小関係を保存して実数体の中に埋め込まれているとする.
![]() は大小関係 < に関して稠密である.なぜなら任意の
は大小関係 < に関して稠密である.なぜなら任意の![]() に対し,
に対し,![]() で仮定から
で仮定から![]() となる
となる![]() が存在する.このとき
が存在する.このとき![]() となるからである.
となるからである.
![]() に対して,実数体の中の数列
に対して,実数体の中の数列![]() を次のように定める.
を次のように定める.![]() で上記議論を用いることにより,自然数
で上記議論を用いることにより,自然数![]() に対して
に対して![]() となる最小の整数
となる最小の整数![]() をとる.
これに対して
をとる.
これに対して
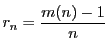 とおく.
とおく.
太郎
この数列は,例えば![]() が整数なら,
が整数なら,![]() は一定ですね.
は一定ですね.
南海
そうだ.そして![]() の稠密性を根拠に,この埋め込みが大小関係を保存することも同様に示される.細部は略する.これによって量空間は実数体
の稠密性を根拠に,この埋め込みが大小関係を保存することも同様に示される.細部は略する.これによって量空間は実数体![]() に埋め込むことができる.量に対応する数の集合は実数で十分であること,つまり実数をはみ出すことはないことがわかる.
に埋め込むことができる.量に対応する数の集合は実数で十分であること,つまり実数をはみ出すことはないことがわかる.
太郎 計量可能な量は,結局実数値をとるのですね.わかりました.
南海 そして,これが逆に実数体の特徴づけになっている.ヒルベルトは実数体を「極大アルキメデス順序体である」として特徴づけた.ヒルベルトのなかには量を実現するに十分な集合としての実数,という考え方があったように思う.
最後に,積の可換性がどのようにして示されるのか,まとめておこう.
数列![]() と
と![]() を基本列とする.
を基本列とする.
i) 基本列は有界である.
数列![]() で,任意の正数
で,任意の正数![]() に対して,
番号
に対して,
番号![]() で,
で,![]() のとき
のとき
![]() となるものが存在する.
となるものが存在する.
![]() を固定すると
を固定すると![]() なら
なら
ii)
![]() となる
となる![]() をとる.
任意の正数
をとる.
任意の正数![]() に対して,
に対して,
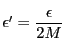 とおき,
この
とおき,
この![]() に対して
に対して![]() のとき
のとき
![]() となる
となる![]() をとる.このとき,
をとる.このとき,
iii) ![]() と
と![]() で定まる実数を
で定まる実数を![]() と
と![]() とし,
その積
とし,
その積![]() を基本列
を基本列![]() で定まる実数として定義する.
で定まる実数として定義する.
その可換性は有理数の可換性![]() の帰結である.
の帰結である.
太郎
「6本のペンを8人分」と「8本のペンを6人分」が等しいことは,1本のペンを![]() とするとき
とするとき
アルキメデスの原理を要請するかぎり,積は可換である以外ありえない.
南海 もとより,これをどのように納得できるように教えるのかは,別の問題であるのだが.
多くのことを学んだが,とりわけ高木貞治が,いかに数を捉えるかについて,生涯の研鑽を積んでいたことを改めて認識し得たことは大きかった.
西洋の自然数にはじまる数の構築に対して,高木貞治の最後の著作となった『数の概念』では,はじめから整数を公理として定義しようとする.より世界的というか,東洋的というか,そういう数の世界をふまえた公理系が示されている.
それは,これまで青空学園でやってきたものより根底的で明晰なものである.また実数の公理についても,数の準備として,いかに他の分野から独立し内在的な定義をするか,最後まで考え続けていた.それを改めて知ることが出来た.
証明は行わないが,その内容のみここで紹介したい.
公理1:![]() は
は![]() 上の全単射写像である.
上の全単射写像である.
公理2:
![]() かつ
かつ![]() ならば
ならば![]() である.
である.
公理3:![]() は無限集合である.
は無限集合である.
ここで集合![]() が無限集合とは,
が無限集合とは,
![]() の真部分集合
の真部分集合![]() で,
で,![]() と
と![]() の間に全単射が存在するものが,
存在することである.
の間に全単射が存在するものが,
存在することである.
太郎
これが整数ですか.….そうか,ペアノの公理で![]() の操作にあたるのが
の操作にあたるのが![]() ですね.
ですね.
南海
![]() でもかまわない.一つの元をとり,それを0とする.
でもかまわない.一つの元をとり,それを0とする.![]() ,
,
![]() .これから整数の諸性質を導くこと自体は,これまでにもやってきたことである.
.これから整数の諸性質を導くこと自体は,これまでにもやってきたことである.
太郎 そして,公理2がペアノの公理の数学的帰納法に対応するものです.
南海 高木貞治は「我々の整数は,物の数でもなく,物の順序を示すものでもない」(『数の概念』)という立場で整数を定義する.数は,数え主義も集合主義もこえているというのである.これは世界的にも他にない一般的な考え方である.
また,19世紀の西洋数学では,あくまで自然数が基礎であり,負数や有理数は逆の存在から必要のために導かれるという立場である.つまり正の数こそ存在する第一のものであり,負数はそこから導かれるという立場である.これにたいして,『数の概念』における定義は,最初から負数も含めた整数の定義である.
太郎 東洋では,伝統的に量とははじめから,両方向にのびるものであったと言われました.そういう東洋の伝統なのでしょうか.
南海 それはわからないが,数学的にも,はじめから整数を定義した方がはるかに簡明である.ペアの以来,というよりギリシア以来,西欧では正の数が存在する量であったが,そのときも東洋では両方向にのびるものとして量がつかまれていた.
だから,もし東洋で近代数学が内部から発展して現れたなら,そのときは自然数からではなく,整数からはじめただろう.高木貞治の半世紀にわたる数の研究の結果として,先祖返りではないが,東洋的な数のつかみ方に至ったことは,たいへん感慨深い.
次に連続体の定義にすすもう.すでに用いてきた用語の定義をまとめる.
1.![]() ,
,![]() ,
,![]() のいずれか一つに定まる.
のいずれか一つに定まる.
2.![]() かつ
かつ![]() ならば,
ならば,![]() である.
である.
ただし,
![]() の最大の元とは,
の最大の元とは,
![]() で任意の
で任意の![]() の元
の元![]() に対して
に対して![]() または
または![]() が成り立つものをいう.
が成り立つものをいう.
無限界性1:![]() は上にも下にも有界ではない.
は上にも下にも有界ではない.
連続性:![]() は連続である.
は連続である.
最小性:連続かつ無限界な全順序集合には,
![]() と同型な部分集合が存在する.
と同型な部分集合が存在する.
これが高木貞治が至った連続体の定義だ.連続体とは,実直線に他ならない.人間は長い歴史を経て,直線というものをこのようにつかんだといえる.
『数とは何か そしてまた何であったか』において足立先生は試案としてさらにもうすこし異なる公理系を立てておられる.それについてはまだまだ議論の余地がありそうだ.まだいまの議論がなされていると言うことだ.
太郎 どのような公理を立てるのかがなぜそんなに問題になるのですか.
南海 公理相互の関係を解明し,可能なかぎり一般的で前提の少ない公理系をうち立てたい.またそのように公理相互の関係を研究すること自体が,そのことを通して実数というものを研究することなのだ.
数学的現象は事実として存在する.それを公理系で捉えようとする.公理は絶対的真理ではなく,数学的な対称をとら得るための方法であり,公理相互の関係の中にその対称の本質的なところが顕れている.