を
の原始関数とするとき, 定積分
を
で定める.となっています.
南海 なるほど.最近はこれを基本定理と書くことはまずない. しかし昔の参考書などには,基本定理と書かれていることも多い. 教科書の記述が,1970年代に大きくかわったのだ. 教科書にどのように書かれているのかということと, 事実として,微分や積分の基本事項は何なのかということを, 考えて見よう.
現在の教科書にはどのように書いてあるのか見てみよう. 手元にあるのは「数研出版」の1997年版の教科書だが, 現在のものと大きくはかわっていない.次のような流れになっている.
そこで,![]() の
の![]() から
から![]() までの定積分を
までの定積分を
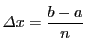 とおくとき,
とおくとき,
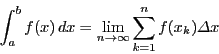
このようになっている.一番重要なところは,(2)である. その証明は教科書によって書かれていたりいなかったりする. それをここで書いておこう.
(2)の証明
![]() と
と![]() 軸および
軸および
![]() を通る
を通る![]() 軸に平行な
2直線で囲まれる図形の面積を
軸に平行な
2直線で囲まれる図形の面積を![]() とおく.
とおく.
![]() に対して増分
に対して増分![]() をとり小区間
をとり小区間
![]() での最小値を
での最小値を
![]() ,最大値を
,最大値を![]() とする.
とする.
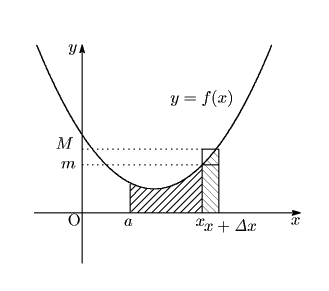
![]() のとき
のとき
![]() である.よって
である.よって
あわせて(3)のはじめのところは次のように示される.
ここで
![]() の原始関数を
の原始関数を![]() とする.
とする.
![]() なので,
なので,
高校数学としては,ここが一番重要なところだ.
史織
すると「![]() と
と![]() 軸に囲まれた図形の面積は,
軸に囲まれた図形の面積は,![]() の
原始関数で求めることができる」ということになります.
これが「微積分の基本定理」なのですか.
の
原始関数で求めることができる」ということになります.
これが「微積分の基本定理」なのですか.
南海 この面積とその導関数の関係は重要で,これを発見するまで, 面積を求めるのに人間はずいぶんと苦労した.
これは大切なことではあるのだが, 教科書では,この面積とその導関数の関係を根拠に,定積分を(2)で, つまり原始関数の値の差として定義する.
史織
しかしそうしてしまうと![]() が成り立つのは当然で,
が成り立つのは当然で,
![]() を基本定理というほどのことはなくなります.
を基本定理というほどのことはなくなります.
どういうことでしょうか.
南海 このように学校では原始関数の値の差として定積分を定義するのだが,実際にそれですべて計算されているかというと, そうではない.最近,掲示板のnayutaさんの投稿で教えられた例を示そう.
史織
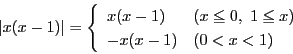
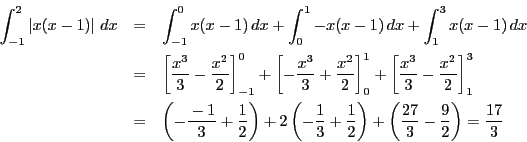
南海
関数
![]() の原始関数
の原始関数![]() は?
は?
史織
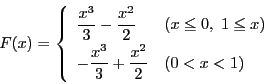
南海
それで![]() を計算すると?
を計算すると?
史織
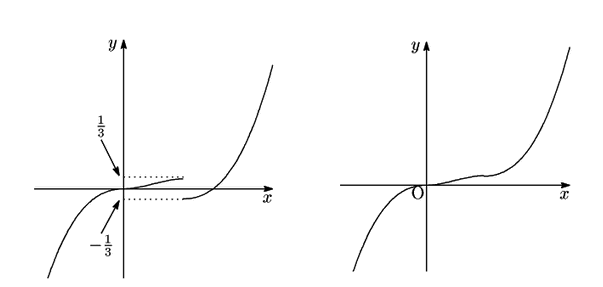
南海 グラフはどうなる.
史織
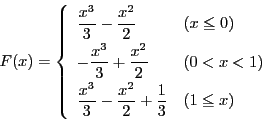
これを![]() に取り直して
に取り直して![]() を計算すると,
を計算すると,
南海 そうなのだ.この場合は面積の方から考えている. だから高校微積の定義と方法は一貫していない. このように,定積分の定義やその意味については, もうすこし深く考えなければならない.
そのために, まず,歴史的に面積を求める方法を振り返ろう.