放物線の面積の問題を初めて始めて解決したのは,アルキメデスだ.アルキメデス (Archimedes,紀元前287〜212)はギリシャ時代後期の人だ. イタリア半島の先の島シシリー島のシラクサに生まれ, エジプトのアレキサンドリアに長く留学し, のち故郷に帰ってそこで一生を過ごした.彼は理論ばかりでなく, その応用にも気を配った. たとえば,時の王ヒーロンが建造した軍艦があまりに大きく, 進水させるのに困っていたときに, 滑車を利用してその軍艦を進水させ,また反射鏡を利用して, おしよせる敵の軍艦を焼き放ったこともある. シラクサがローマ軍の侵攻を受けたときには, 石を飛ばす機械などの武器を発明して敵軍をおおいに悩ませた.
しかし,シラクサもついに落城の日を迎えてしまった. シシリー島にせめこんだローマの軍隊はこの天才を殺してしまった. プルタークの『英雄伝』は次のようにその最期を記す. 「アルキメデスは自分の家で図形を見ながら何か考えていた. 心も顔もその研究に注いでいたので, ローマ軍が侵入したことも町が陥落したことも気づかずにいた. 突然一人の兵隊がそこに来てアルキメデスへついて来いと命令した. だがアルキメデスはその問題を解いて証明を得ないうちは行こうとしなかった. 兵隊は腹を立てて剣を抜いて刺し殺してしまった」. また「兵士の1人が彼の研究中の円をふんだので, 思わず『その円をふむな』と叫んだところ,槍で刺されてしまった.」 ともいわれている.
アルキメデスの逸話のなかで最も有名なのは, ヒーロン王の王冠の話である. ヒーロン王はあるとき,鍛冶屋に純金をわたして, それで王冠を作るように命じた.王冠はみごとにできあがったが, しかしこの鍛冶屋は,渡された純金を全部使わないで, それに混ぜ物をして王冠を作ったのではないかという噂が流れた. そこでヒーロン王は,アルキメデスに命じて, この王冠が果して純金だけでできているか, それとも混ぜ物がしてあるかを調べさせた.
大切な王冠をあずかったアルキメデスは,それを傷つけることなく, 純金だけでできているか,混ぜ物がしてあるかの判定法を見出すのに日夜苦心した. ある日浴場で,湯のなかでは,自分の身体が少し軽くなることに気づいた. これから彼は「物体は,水中では, それと同体積の水の目方だけ軽くなる」という, いわゆるアルキメデスの原理を思いついたといわれる. これを利用すれば,王冠の鑑別ができることに気づいたアルキメデスは, 「私は発見した」と叫びながら,裸で家まで走って帰ったという.
この原理から,王冠の空中での重さ![]() と水中での重さ
と水中での重さ![]() の差として王冠の体積
の差として王冠の体積![]() がわ
かる.比重がわかり,純金の比重と比べれば混ぜ物が入っているかどうかわかるのだ.
がわ
かる.比重がわかり,純金の比重と比べれば混ぜ物が入っているかどうかわかるのだ.
この時代は,もちろん座標の方法もないし,
関数を式に表すことも知られていない.
彼は放物線で囲まれた図形の面積を次のように求めた.
一応座標に入れて説明するが,アルキメデスはもっと図形的にやったのである.
放物線の方程式を![]() とする.
とする.
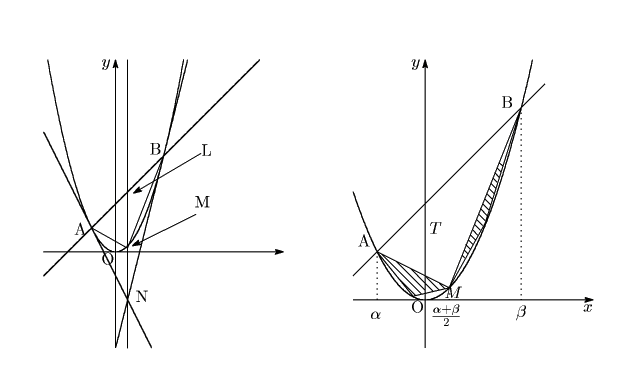
![]() 座標が
座標が![]() と
と![]() の
の![]() 座標の中点と一致する点を
座標の中点と一致する点を![]() ,
,
![]() と
と![]() での接線の交点を
での接線の交点を![]() とする.
このとき一般に
とする.
このとき一般に
彼は次のように示した.
右側の図の斜線部分の面積はちょうど![]() である(なぜか?).
ここで斜線部分に対して同じ操作を行うとさらに
である(なぜか?).
ここで斜線部分に対して同じ操作を行うとさらに
![]() 面積が増える.
このようにして次々に加えていくとこの面積の和は
面積が増える.
このようにして次々に加えていくとこの面積の和は![]() に近づく.つまり
に近づく.つまり
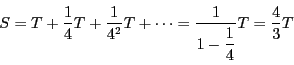
史織
![]() の座標は
の座標は
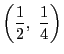 なので
なので
南海
だから
史織 わー,たいへんですね.
放物線と,2点A,Bから![]() 軸への垂線と,
軸への垂線と,![]() 軸で囲まれた
図形の面積を,ここでは
軸で囲まれた
図形の面積を,ここでは![]() とします.
Bの方を動点にして,面積を
とします.
Bの方を動点にして,面積を![]() とする.
とする.
面積を求めるときに
![]() がいかに大切なのか,その意味がわかります.
これを知ってれば
がいかに大切なのか,その意味がわかります.
これを知ってれば![]() は
は
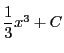 なので
なので
![\begin{displaymath}
U(2)=\biggl[\dfrac{1}{3}x^3\biggr]_{-1}^2=3
\end{displaymath}](images/img78.gif)
南海 そうだ.